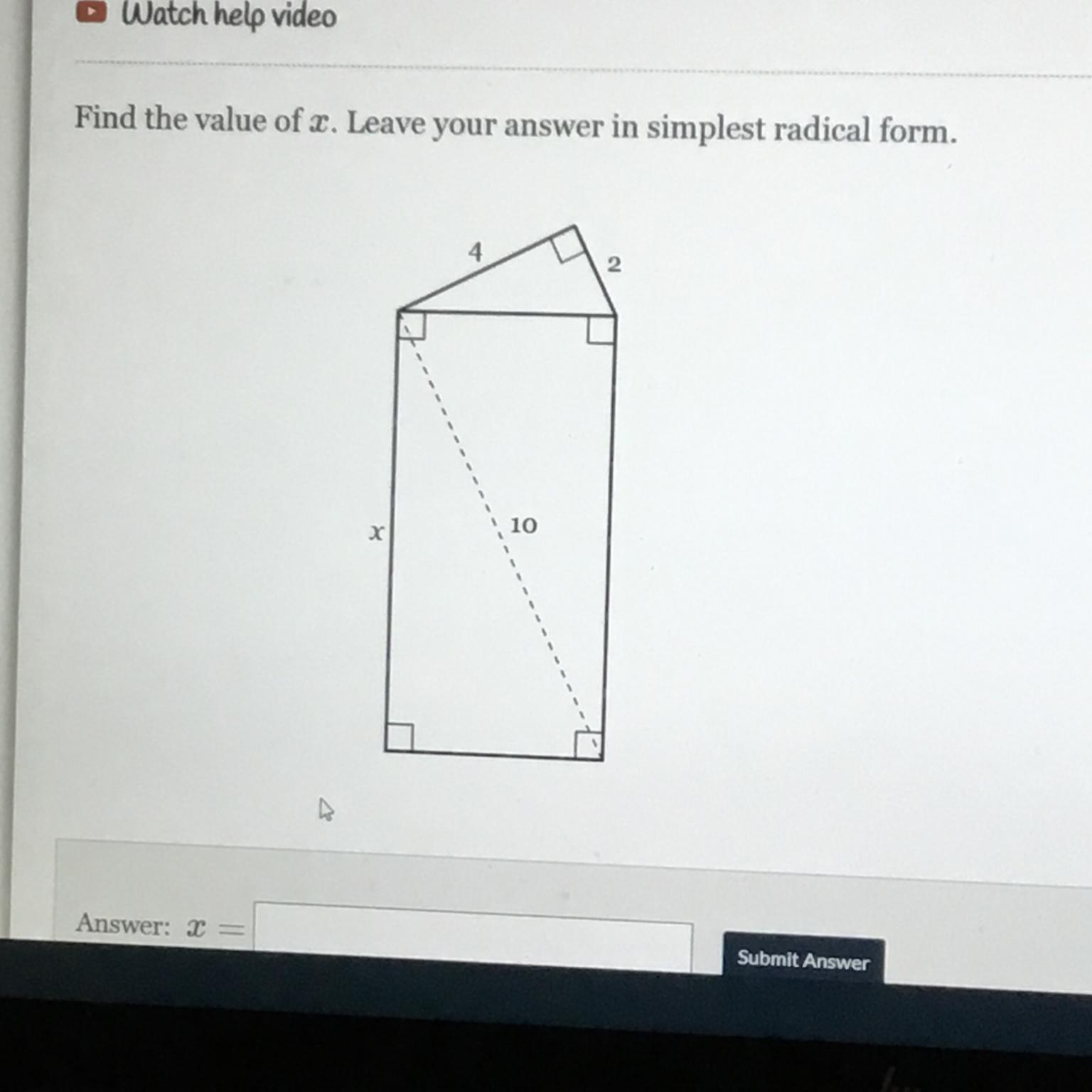
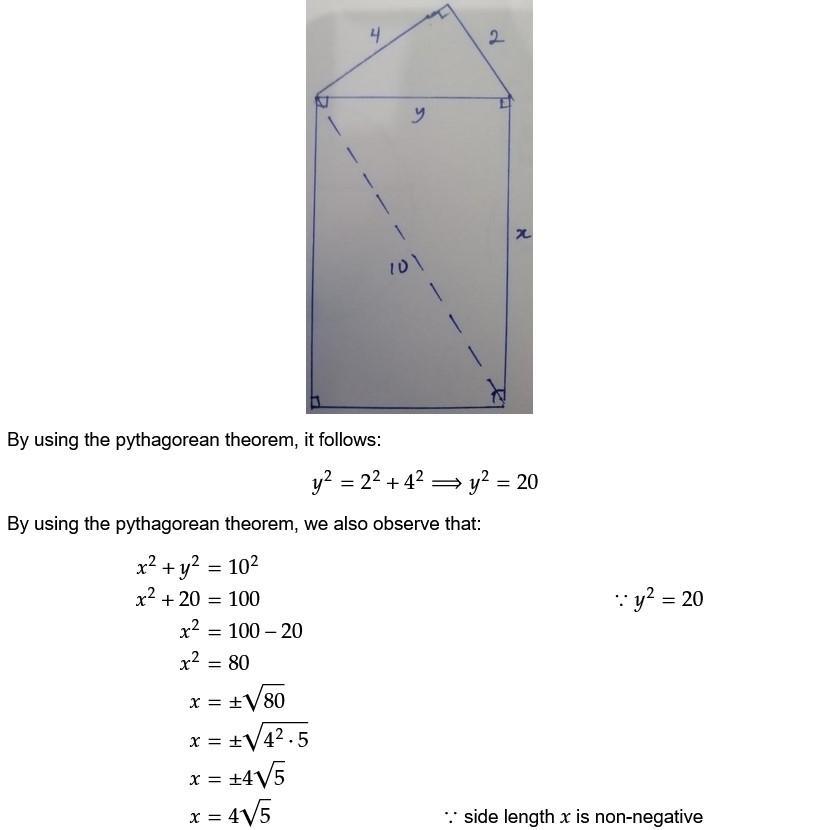
Answers
Answer: [tex]x=4\sqrt{5}[/tex]
Step-by-step explanation:
The explanation is attached below.
Related Questions
transform the basis b = {v1 = (4, 2), v2 = (1, 2)} of r 2 into an orthonormal basis whose first basis vector is in the span of v1.
Answers
The given basis is b = [tex]b = {v_1 = (4,2), v_2 = (1,2)}[/tex]. The orthonormal basis we obtain is {[tex]u_1[/tex], [tex]u_2[/tex]} = {(1/5, 1/10), (1, 18/23)}.
To transform this basis into an orthonormal basis, we can use the Gram-Schmidt process.
Gram-Schmidt process
Step 1:
The first step is to normalize [tex]v_1[/tex].
We can obtain a unit vector in the direction of [tex]v_1[/tex] by dividing [tex]v_1[/tex] by its magnitude:
[tex]u_1 = v_1/||v_1|| = (4,2)/sqrt(4^2+2^2) = (4/20, 2/20) = (1/5, 1/10)[/tex]
Step 2: We now need to find a vector that is orthogonal to u1 and in the span of [tex]v_2[/tex].
To achieve this, we can subtract the projection of [tex]v_2[/tex] onto [tex]u_1[/tex] from [tex]v_2[/tex]:
v₂₋₁ = v₂ - (v₂.u₁)u₁
Here, [tex]v_2.u_1[/tex] represents the dot product of [tex]v_2[/tex] and [tex]u_1.v_2.u_1[/tex] = (1,2).(1/5,1/10)
= 2/5So,
v₂₋₁ = v₂ - (2/5)u₁
= (1,2) - (2/5)(1/5,1/10)
= (1-2/25, 2-1/5)
= (23/25, 9/10)
Step 3: We now normalize [tex]V_2_1[/tex] to obtain a second unit vector: [tex]u_2=v_2_1/||v_2_1||[/tex]
= [tex](23/25, 9/10)\sqrt((23/25)^2 + (9/10)^2)[/tex]
= (23/25, 9/10)/(23/25)
= (1, 18/23)
So the orthonormal basis we obtain is {[tex]u_1[/tex], [tex]u_2[/tex]} = {(1/5, 1/10), (1, 18/23)}.
To know more about orthonormal, visit:
https://brainly.com/question/31992754
#SPJ11
Find the solution to the boundary value problem: d²y/dt² = 8 dy/dt + 15y = 0, y(0) = 9, y(1) = 9 The solution is y =
Answers
The given differential equation is a second-order linear homogeneous differential equation. To solve this boundary value problem, we can use the method of characteristic equations.
First, we find the characteristic equation by substituting y = e^(rt) into the differential equation: r^2 - 8r + 15 = 0 Solving the quadratic equation, we find the roots: r1 = 3 and r2 = 5. The general solution to the homogeneous equation is y(t) = C1e^(3t) + C2e^(5t), where C1 and C2 are constants.
Next, we apply the boundary conditions y(0) = 9 and y(1) = 9:
y(0) = C1e^(30) + C2e^(50) = C1 + C2 = 9
y(1) = C1e^(31) + C2e^(51) = C1e^3 + C2e^5 = 9
We have two equations with two unknowns (C1 and C2), and we can solve this system of equations to find the values of C1 and C2. Solving the equations, we find C1 = 9/(e^3 - e^5) and C2 = 9/(e^5 - e^3). Therefore, the solution to the boundary value problem is y(t) = (9/(e^3 - e^5))e^(3t) + (9/(e^5 - e^3))e^(5t).
Learn more about homogeneous equations here: brainly.com/question/9576391
#SPJ11
A coin is tossed twice. Let Z denote the number of heads on the first toss and W the total number of heads on the 2 tosses. If the coin is unbalanced and a head has a 40% chance of occurring, find
(a) the joint probability distribution of W and Z;
(b) the marginal distribution of W;
(c) the marginal distribution of Z;
(d) the probability that at least 1 head occurs.
Answers
The joint probability distribution of W and Z for two coin tosses, where the probability of heads is 0.4, is as follows:
P(W=0, Z=0) = 0.36
P(W=1, Z=1) = 0.16
P(W=1, Z=0) = 0.48
P(W=2, Z=0) = 0.16
The joint probability distribution of W and Z reveals the probabilities of different outcomes when tossing a biased coin twice. With a 40% chance of heads, we find that the probability of both tosses resulting in tails is 0.36, the probability of getting one head on the first toss and one head on the second toss is 0.16, the probability of getting one head on the first toss and no head on the second toss (or vice versa) is 0.48, and the probability of getting two heads is 0.16.
Learn more about probability here : brainly.com/question/31828911
#SPJ11
For
the game below create...
a) a probability distribution chart in the form of x, p(x),
x•p(x), $ amount won • probability of winning for each assigned
number
!!Keep inGame Description Entry fee: $7 Stage 1: Roll a die and get assigned a number (1, 2, 3, 4,5, or 6) Stage 2: Divided into 4 trials (excluding the one from stage 1) Roll the number you were assigned from stage 1, twice (or 3 or 4 times (prize remains the same either way)) and win. Don't roll that same number from stage 1 or you roll a different number twice etc.; you lose Game rules: You don't have to roll the assigned number 2 times in a row; it doesn't have to be consecutive. You do not get a prize for landing on a number "close" to yours. Prizes: Get assigned #1 in stage I then roll it at least 2 times within stage 2 and earn $2. Get assigned #2 in stage 1 then roll it at least 2 times within stage 2 and carn $4. Etc. In simpler terms... 1: $2 2: S4 3: $6 4: $8 5: $10 6: $12 E(X)=rx a/n = 4 (# of trials) * 6 (desired outcomes) / 24 (# of outcomes) = 24/24 = 1 E(X)*0.. game is not fair
Expert Answer
Answers
Now, we can calculate the expected value, E(X) and prize money earned per game (E(X)*0.75) using the probability distribution chart.
The probability distribution chart of the game is given below:
Number of times rolled (x) Probability of winning (P(x)) Prize ($) E(X) = xP(x) Prize ($) * Probability of winning (E(X)*0.75)1 (5/36) 2 0.139 0.10425 2 (4/36) 4 0.222 0.16650 3 (3/36) 6 0.250 0.18750 4 (2/36) 8 0.222 0.16650 5 (1/36) 10 0.139 0.10425 6 (1/36) 12 0.028 0.02100 Total 1.000 0.75000
We can see that E(X) value is not equal to the value of prize money earned per game, i.e., $5.63. Therefore, the game is not a fair game.
The value of E(X) is calculated as follows:
E(X)=rx a/n
= 4*6/24
= 1.
The probability of winning the game is calculated as follows:
Probability (P) = number of successful outcomes / total number of outcomes
The number of total outcomes = 6 (the number of outcomes of the first stage).
The number of successful outcomes = 5 (the same assigned number) x 5 (the number of possible outcomes from the second stage)/ 36 (the total number of possible outcomes).
P(x) = 5/36 when x = 1P(x) = 4/36 when x = 2P(x) = 3/36 when x = 3P(x) = 2/36 when x = 4P(x) = 1/36 when x = 5P(x) = 1/36 when x = 6
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
10. If an airplane travels at an average speed of 510 mph, how far does the airplane move in 50 minutes? O A. 400 miles O B. 500 miles O C. 425 miles O D. 475 miles
Answers
The airplane moves 425 miles in 50 minutes.
Hence the correct option is (C). 425 miles.
Given that an airplane travels at an average speed of 510 mph.
We need to find how far the airplane moves in 50 minutes.
Solution:
We know that the average speed of the airplane = Distance/Time.
So, Distance = Speed × Time.
The speed of the airplane is given as 510 mph.
And, the time duration is given as 50 minutes.
In order to convert the time from minutes to hours, we will divide it by 60.
Therefore, the time in hours is 50/60 hours = 5/6 hours.
Substitute the values in the formula.
Distance = 510 × 5/6
= 425 miles.
To know more about the Average speed, visit:
https://brainly.com/question/10449029
#SPJ11
Find () (n), then state the domain and range. Given, h(n) = -4n²+1 g(n)=-n³ + 2n²
Answers
The composite function is h(g(n)) = -4n⁶ + 16n⁵ - 16n⁴ + 4n² + 1, and the domain and range of h(g(n)) are both (-∞, ∞)
To find h(g(n)), we will substitute g(n) into h(n).
Therefore,
h(g(n)) = -4g(n)² + 1
= -4(-n³ + 2n²)² + 1
= -4n⁶ + 16n⁵ - 16n⁴ + 4n² + 1
Now, let's determine the domain and range of h(g(n)).
The domain of h(g(n)) is the same as the domain of g(n), which is all real numbers.
Therefore, the domain is (-∞, ∞).
The range of h(g(n)) is the set of all possible values of h(g(n)).
Since h(g(n)) is a polynomial function, its range is also all real numbers.
Therefore, the range is also (-∞, ∞).
Therefore, the domain and range of h(g(n)) are both (-∞, ∞).
In conclusion, h(g(n)) = -4n⁶ + 16n⁵ - 16n⁴ + 4n² + 1, and the domain and range of h(g(n)) are both (-∞, ∞)
Know more about the composite function
https://brainly.com/question/10687170
#SPJ11
Select the correct choice. The discriminant of ax² + bx + c = 0 is defined as 2 OA. 2a OB. b² - 4ac OC. -b OD. √√b²-4ac 2
Answers
The discriminant of ax² + bx + c = 0 is defined as b² - 4ac. Hence, the correct option is OB. b² - 4ac
The discriminant is a mathematical expression that aids in the evaluation of the roots of a quadratic equation.
To be more precise, the quadratic formula (x = -b ± √b²-4ac/2a) uses the discriminant.
The discriminant is represented as D=b²-4ac.
The value of the discriminant reveals critical information about the quadratic equation.
It is possible to classify a quadratic equation's roots into various types depending on the discriminant's value.
The formula for finding the roots of the quadratic equation is provided below. When using this formula, it is critical to remember the discriminant.
The correct option is OB. b² - 4ac
Know more about the discriminant
https://brainly.com/question/24730520
#SPJ11
Consider the linear DE y"+2y=2 cos²x. According to the undetermined coefficient method, the particular solution of the given DE is? 1. sin.x II. cos x III. sin² x IV. sin.x.cos.x V. sin x- cos x
Answers
To find the particular solution of the given linear differential equation using the undetermined coefficient method, we assume the particular solution to have the same form as the non-homogeneous term, which is 2 cos²x.
The form of the particular solution can be expressed as:
y_p = A cos²x + B cosx + C
Taking the derivatives of y_p, we have:
y_p' = -2A sinx cosx - B sinx
y_p'' = -2A cos²x + 2A sin²x - B cosx
Substituting these derivatives into the differential equation, we get:
(-2A cos²x + 2A sin²x - B cosx) + 2(A cos²x + B cosx + C) = 2 cos²x
Simplifying the equation, we obtain:
(2A - B) cos²x + (2A + 2C) cosx + (2A - 2B) sin²x = 2 cos²x
Comparing the coefficients of cos²x, cosx, and sin²x, we have:
2A - B = 2
2A + 2C = 0
2A - 2B = 0
From the second equation, we find A = -C, and substituting this into the third equation, we get B = A.
Therefore, the particular solution y_p is given by:
y_p = A cos²x + A cosx - A
Considering the available options, the particular solution can be written as:
y_p = -cos²x - cosx + 1
Thus, the correct choice is V. sin x - cos x.
To learn more about Derivatives - brainly.com/question/25324584
#SPJ11
State Y State Z 12.4 19.5 8.7 7,400 44,800 47,200 Population (in millions) Land ama (sqante miles) Number of state parks Per capita income 120 178 36 $50,313 $49,578 $46,957 Based on the information given, which of the following statements are true for States X, Y, and Z? Indicate all such statements. The population is greatest for State Y. The per capita income is greatest for State Z. The number of people per state park is greatest for State Z.
Answers
Based on the information provided, the following statements are true for States X, Y, and Z: the population is greatest for State Y, the per capita income is greatest for State X, and the number of people per state park is greatest for State Z.
According to the given data, State Y has the highest population of 12.4 million, making the statement "The population is greatest for State Y" true. However, the per capita income is not provided for State Z, so we cannot determine if the statement "The per capita income is greatest for State Z" is true or false. State X has the highest per capita income of $50,313, which makes the statement false.
The number of people per state park can be calculated by dividing the population by the number of state parks. For State X, the calculation is 12.4 million divided by 120 state parks, which gives approximately 103,333 people per state park. For State Y, the calculation is 19.5 million divided by 178 state parks, which gives approximately 109,551 people per state park. For State Z, the calculation is 8.7 million divided by 36 state parks, which gives approximately 241,667 people per state park. Therefore, the statement "The number of people per state park is greatest for State Z" is true.
In conclusion, based on the given information, the population is greatest for State Y, the per capita income is greatest for State X, and the number of people per state park is greatest for State Z.
Learn more about per capita income here:
https://brainly.com/question/31234289
#SPJ11
A polynomial f(x) and two of its zeros are given. f(x) = 2x³ +11x² +44x³+31x²-148x+60; -2-4i and 11/13 are zeros Part: 0 / 3 Part 1 of 3 (a) Find all the zeros. Write the answer in exact form.
Answers
Given that f(x) = 2x³ + 11x² + 44x³ + 31x² - 148x + 60; -2 - 4i and 11/13 are the zeros. The zeros of the given polynomial are -2 - 4i, 11/13, and -2 + 4i.
The given polynomial is f(x) = 2x³ + 11x² + 44x³ + 31x² - 148x + 60.
Thus, f(x) can be written as 2x³ + 11x² + 44x³ + 31x² - 148x + 60 = 0
We are given that -2 - 4i and 11/13 are the zeros. Let's find out the third one. Using the factor theorem,
we know that if (x - α) is a factor of f(x), then f(α) = 0.
Let's consider -2 + 4i as the third zero. Therefore,(x - (-2 - 4i)) = (x + 2 + 4i) and (x - (-2 + 4i)) = (x + 2 - 4i) are the factors of the polynomial.
So, the polynomial can be written as,f(x) = (x + 2 + 4i)(x + 2 - 4i)(x - 11/13) = 0
Now, let's expand the above equation and simplify it.
We get, (x + 2 + 4i)(x + 2 - 4i)(x - 11/13) = 0
⇒ (x + 2)² - (4i)²(x - 11/13) = 0 (a² - b² = (a+b)(a-b))
⇒ (x + 2)² + 16(x - 11/13) = 0 (∵ 4i² = -16)
⇒ x² + 4x + 4 + (16x - 176/13) = 0
⇒ 13x² + 52x + 52 - 176 = 0 (multiply both sides by 13)
⇒ 13x² + 52x - 124 = 0
⇒ 13x² + 26x + 26x - 124 = 0
⇒ 13x(x + 2) + 26(x + 2) = 0
⇒ (13x + 26)(x + 2) = 0
⇒ 13(x + 2)(x + 2i - 2i - 4i²) + 26(x + 2i - 2i - 4i²) = 0 (adding and subtracting 4i²)
⇒ (x + 2)(13x + 26 + 52i) = 0⇒ x = -2, -2i + 1/2 (11/13)
Therefore, the zeros of the given polynomial are -2 - 4i, 11/13, and -2 + 4i.
Read more about polynomial
https://brainly.com/question/11536910
#SPJ11
full step by step solution please
Question 1: COS²0 Sin ² 6 = 1 between 0L 0 ≤ 2п Sin ¹8=1- Cos A Cos 1+ sin e
. Value of e
Answers
To find the value of e in the given equation:
COS²0 Sin ² 6 = 1 between 0L 0 ≤ 2п Sin ¹8=1- Cos A Cos 1+ sin e
Let's break down the equation and solve step by step:
Start with the equation: COS²0 Sin ² 6 = 1 between 0L 0 ≤ 2п Sin ¹8=1- Cos A Cos 1+ sin e
Simplify the trigonometric identities:
COS²0 Sin ² 6 = 1 (using the Pythagorean identity: sin²θ + cos²θ = 1)
Substitute the value of 6 for e in the equation:
COS²0 Sin²(π/6) = 1
Evaluate the sine and cosine values for π/6:
Sin(π/6) = 1/2
Cos(π/6) = √3/2
Substitute the values in the equation:
COS²0 (1/2)² = 1
COS²0 (1/4) = 1
Simplify the equation:
COS²0 = 4 (multiply both sides by 4)
COS²0 = 4
Take the square root of both sides:
COS0 = √4
COS0 = ±2
Since the range of the cosine function is [-1, 1], the value of COS0 cannot be ±2.
Therefore, there is no valid solution for the equation.
To know more about values visit-
brainly.com/question/31988937
#SPJ11
Urgently! AS-level Maths
Two events A and B are mutually exclusive, such that P(A) - 0.2 and P(B) = 0.5. Find (a) P(A or B), Two events C and D are independent, such that P(C)-0.3 and P(D)-0.6. Find (b) P(C and D). (1) (1) (T
Answers
a) The two events A and B are mutually exclusive and the probability of A occurring is P(A) = 0.2, and the probability of event B occurring is
P(B) = 0.5.
The probability of A or B happening is given by the following formula:
P(A or B) = P(A) + P(B) – P(A and B)
Since the two events are mutually exclusive, it means they cannot happen at the same time, so
P(A and B) = 0.
Thus,
P(A or B) = P(A) + P(B)
= 0.2 + 0.5
= 0.7
b) The events C and D are independent of each other and the probability of event C happening is
P(C) = 0.3,
while the probability of event D occurring is
P(D) = 0.6.
The probability of C and D happening is given by:
P(C and D) = P(C) x P(D)
= 0.3 x 0.6
= 0.18
Answer: a) P(A or B) = 0.7,
b) P(C and D) = 0.18
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
│u│= 11, │v│= 17 and the angle between and (when placed tail-to-tail) is 63°. Find │2u+v│=
a. √410
b. b) 28
c. 39
d. 33.36
Answers
The calculated magnitude of the vector |2u + v| is (d) 33.36
How to calculate the magnitude of the vector |2u + v|From the question, we have the following parameters that can be used in our computation:
|u| = 11
|v| = 17
Also, we have
Angle, θ = 63 degrees
The vector |2u + v| is then calculated using the following law of cosines
|2u+v|² = (2 * |u|)² + |v|² + 2 * 2 * |u| * |v| * cos(63°)
substitute the known values in the above equation, so, we have the following representation
|2u+v|² = (2 * 11)² + 17² + 2 * 2 * 11 * 17 * cos(63°)
Evaluate
|2u+v|² = 1112.58
Take the square root of both sides:
|2u+v| = 33.355
Approximate
|2u+v| = 33.36
Hence, the magnitude of the vector |2u + v| is (d) 33.36
Read more about vector at
https://brainly.com/question/12911469
#SPJ4
Sarah invests $1000 at time O into an account that accumulates interest at an annual effective discount rate of 8%. Two years after Sarah's investment, Erin deposits X into an account that gains interest at a nominal interest rate of 9% compounded semiannually. Eight years after Sarah's initial investment, Erin's account is worth twice as much as Sarah's account. Find X. Round your answer to the nearest .xx
Answers
Sarah invests $1000 at time 0 into an account that accumulates interest at an annual effective discount rate of 8%. Erin deposits X into an account that gains interest at a nominal interest rate of 9% compounded semiannually. Two years after Sarah's investment.
Erin deposits X into an account that gains interest at a nominal interest rate of 9% compounded semiannually, i.e. after 2 years, Sarah's account will worth [tex]$1000(1 - 8%)²[/tex][tex])[/tex] Erin's account is worth twice as much as Sarah's account after 8 years.
Therefore, Erin's invests of X will be worth [tex]$1000(1 - 8%)² * 2[/tex][tex])[/tex] in 8 years. Erin's investment grows at a nominal rate of 9% compounded semiannually for 8 years, i.e. Erin's investment after 8 years will be worth [tex]X(1 + 4.5%)¹⁶[/tex][tex])[/tex] .On equating the above 2 expressions we get;[tex]X(1 + 4.5%)¹⁶ = $1000(1 - 8%)² * 2= > X = ($1000(1 - 8%)² * 2) / (1 + 4.5%)¹⁶≈ $526.11.\[/tex][tex])[/tex]
To know more about invests visit:
https://brainly.com/question/17252319
#SPJ11
If there is no seasonal effect on human births, we would expect equal numbers of children to be born in each season (winter, spring, summer, and fall). A student takes a census of her statistics class and finds that of the 120 students in the class, 26 were born in winter, 34 in spring, 32 in summer, and 28 in fall. She wonders if the excess in the spring is an indication that births are not uniform throughout the year.
a) What is the expected number of births in each season if there is noseasonal effect on births?
b) Compute the $\chi^2$ statistic.
c) How many degrees of freedom does the $\chi^2$ statistic have?
Answers
The chi-square statistic for the observed births in different seasons of the statistics class is approximately 1.3333 with 3 degrees of freedom, suggesting that there might be a deviation from the expected uniform distribution.
a) If there is no seasonal effect on births, we would expect an equal number of births in each season. Since there are 120 students in the class, the expected number of births in each season would be 120 divided by 4, which is 30 births in each season.
b) To compute the chi-square statistic, we need to compare the observed frequencies (26, 34, 32, and 28) with the expected frequencies (30, 30, 30, and 30). The chi-square statistic formula is:
χ² = Σ((O - E)² / E)
where O is the observed frequency and E is the expected frequency.
Let's calculate the chi-square statistic:
χ² = ((26 - 30)² / 30) + ((34 - 30)² / 30) + ((32 - 30)² / 30) + ((28 - 30)² / 30)
= (4² / 30) + (4² / 30) + (2² / 30) + (2² / 30)
= (16 / 30) + (16 / 30) + (4 / 30) + (4 / 30)
= 0.5333 + 0.5333 + 0.1333 + 0.1333
≈ 1.3333
Therefore, the chi-square statistic is approximately 1.3333.
c) The degrees of freedom for the chi-square test can be calculated as (number of categories - 1). In this case, there are four seasons, so the degrees of freedom would be (4 - 1) = 3.
Therefore, the chi-square statistic has 3 degrees of freedom.
To know more about chi-square statistic,
https://brainly.com/question/31036507
#SPJ11
Tracy is studying an unlabeled dataset with two features 21, 22, which repre- sent students' preferences for BTS and dogs, respectively, each on a scale from 0 to 100. The dataset is plotted in the visualization to the right: Student Preference for Dogs 25 ܂܆ܟ 0 0 10 20 30 Student Preference for BTS (a) [2 Pts) Tracy would like to experiment with supervised and unsupervised learning methods. Which of the following is a supervised learning method? Select all that apply. A. Logistic regression B. Linear regression I C. Decision tree OD. Agglomerative clustering E. K-Means clustering
Answers
Supervised learning methods require labeled data.
The goal is to predict a target variable based on the input variables using a model. Logistic regression and linear regression are examples of supervised learning algorithms. As a result, options A and B are supervised learning methods.
Agglomerative clustering and K-Means clustering are unsupervised learning methods. These methods are used to find hidden structures or patterns in data.
Summary: Supervised learning is a machine learning algorithm that is trained using labeled data. Logistic regression and linear regression are examples of supervised learning algorithms. Therefore, Options A and B are supervised learning methods. On the other hand, Agglomerative clustering and K-Means clustering are unsupervised learning methods.
Learn more about regression click here:
https://brainly.com/question/25987747
#SPJ11
Prove that for all n € N, the formula a’n = 3(-2)^n + n(2)^n + 5 satisfies the recurrence relation a0 = 8, a1 = 1, a2 = 25,
ל an = 2an-1 + 4an-2 - 8an-3 + 15.
Answers
The sequence satisfies the recurrence relation a0 = 8, a1 = 1, a2 = 25, ל an = 2an-1 + 4an-2 - 8an-3 + 15 and the given formula a′n = 3(−2)n + n(2)n + 5.
The proof that for all n € N, the formula a′n = 3(−2)n + n(2)n + 5 satisfies the recurrence relation
a0 = 8,
a1 = 1,
a2 = 25,
an = 2an−1 + 4an−2 − 8an−3 + 15
is given below:
Formula to be proved:
a′n = 3(−2)n + n(2)n + 5
Recurrence relation:
an = 2an-1 + 4an-2 - 8an-3 + 15
Given values:
a0 = 8, a1 = 1, a2 = 25
We'll begin with n = 0 to prove the given formula.
Substitute n = 0 in a′n = 3(−2)n + n(2)n + 5 to obtain:
a'0 = 3(−2)0 + 0(2)0 + 5
= 3 + 5
= 8
Substitute n = 0 in an = 2an-1 + 4an-2 - 8an-3 + 15 to obtain:
a0 = 2a-1 + 4a-2 - 8a-3 + 15... (Equation A)
Now, substitute a0 = 8 in Equation A to obtain:
8 = 2a-1 + 4a-2 - 8a-3 + 15... (Equation B)
Rearrange Equation B to obtain:
8 - 15 = 2a-1 + 4a-2 - 8a-3 - 7-7
= 2a-1 + 4a-2 - 8a-3
Divide both sides by -2 to obtain:
a-1 + 2a-2 - 4a-3 = 3
Substitute n = 1 in a′n = 3(−2)n + n(2)n + 5 to obtain:
a'1 = 3(−2)1 + 1(2)1 + 5 = -1
Now, substitute a1 = 1 in the recurrence relation to obtain:
a1 = 2a0 + 4a-1 - 8a-2 + 15
We know that a0 = 8, substitute it to get:
1 = 2(8) + 4a-1 - 8a-2 + 15
Rearrange and simplify to obtain:
a-1 - 2a-2 = -4
Substitute n = 2 in a′n = 3(−2)n + n(2)n + 5 to obtain:
a'2 = 3(−2)2 + 2(2)2 + 5 = 21
Now, substitute a2 = 25 in the recurrence relation to obtain:
a2 = 2a1 + 4a0 - 8a-1 + 15
Substitute a1 = 1 and a0 = 8 to obtain:
25 = 2(1) + 4(8) - 8a-1 + 15
Rearrange and simplify to obtain: a-1 = -5
Substitute a-1 = -5 and a-2 = 4 in a-1 + 2a-2 - 4a-3 = 3 to obtain:
(-5) + 2(4) - 4a-3
= 3a-3
= 1
Know more about the recurrence relation
https://brainly.com/question/4082048
#SPJ11
let us consider a sample space ω = {ω1,...,ωn} of size n > 2 and two probability functions p1 and p2 on it. that is, we have two probability spaces: (ω,p1) and (ω,p2)
Answers
the sample space for both the probability spaces is the same, i.e., ω = {ω1, ..., ωn} and the probability function maps from this sample space to the interval [0,1]
Given the sample space ω = {ω1, ..., ωn} of size n > 2 and two probability functions p1 and p2 on it, the two probability spaces are: (ω, p1) and (ω, p2).
Sample space is a concept in probability theory, statistics, and other related fields that describes the set of all possible outcomes or events of an experiment or random occurrence. It is represented by the letter “S”.
Definition of Probability Space: A probability space is defined by a sample space and a probability function on that sample space. It is represented by the letter “(ω, p)”.
Definition of Probability Function: Probability function is defined as a function that maps from the sample space to the interval [0,1], i.e., p:
S → [0,1], such that it satisfies the following three axioms:
For any event A, 0 ≤ P(A) ≤ 1.P(Ω)
= 1.P(A1 ∪ A2 ∪ ...)
= P(A1) + P(A2) + ...,
where A1, A2, ... are mutually exclusive (disjoint) events.
Given, two probability functions p1 and p2 on the sample space
ω = {ω1, ..., ωn} of size n > 2.
Thus, we have two probability spaces: (ω, p1) and (ω, p2).
Therefore, the sample space for both the probability spaces is the same, i.e.,
ω = {ω1, ..., ωn} and the probability function maps from this sample space to the interval [0,1].
Since p1 and p2 are probability functions, they satisfy the three axioms mentioned above.
To know more about probability visit :
https://brainly.com/question/31828911
#SPJ11
Find a particular solution to the differential equation using the method of Undetermined Coefficients. *"'() - 8x"(t) + 16x(t)= 5te 4 A solution is xy(t)=0
Answers
A particular solution to the given differential equation is [tex]Xp\left(t\right)\:=\:-24t^2e^{4t}[/tex]
To find a particular solution using the Method of Undetermined Coefficients, we assume a particular solution of the form:
[tex]Xp\left(t\right)\:=\:At^2e^{4t}[/tex]
Now, let's differentiate Xp(t) to find the first and second derivatives:
[tex]Xp'\left(t\right)\:=\:\left(2At^2+\:8At\right)e^{4t}[/tex]
[tex]Xp''\left(t\right)\:=\:\left(2A\:+\:8At\:+\:8A\right)t^2.e^{4t}+\:\left(16At\:+\:8A\right)e^{4t}[/tex]
Substituting these derivatives into the original differential equation, we have:
[tex]\left(2A\:+\:8At\:+\:8A\right)t^2e^{4t}\:+\:\left(16At\:+\:8A\right)e^{4t}-\:8\left(2At^2+\:8At\right)e^{4t}\:+\:16\left(At^2e^{4t}\right)\:=\:144t^2e^{4t}[/tex]
Simplifying and collecting like terms, we get:
[tex]\left(2A\:+\:8At\:+\:8A\:-\:16A\right)t^2e^{4t}\:+\:\left(16At\:+\:8A\:-\:16A\right)e^{4t}\:=\:144t^2e^{4t}[/tex]
Now, equating the coefficients of like terms on both sides, we have:
[tex]\left(2A\:-\:8A\right)t^2e^{4t}\:+\:\left(16A\:-\:8A\right)e^{4t}\:=\:144t^2e^{4t}[/tex]
[tex]-6At^2e^{4t}+\:8Ae^{4t}\:=\:144t^2e^{4t}[/tex]
To make the left side equal to the right side, we must have:
-6At² + 8A = 144t²
Comparing the coefficients of t² on both sides, we get:
-6A = 144 => A = -24
Therefore, a particular solution to the given differential equation is:
[tex]Xp(t) = -24t^2e^(^4^t)[/tex]
To learn more on Differentiation click:
https://brainly.com/question/24898810
#SPJ4
-2 2-4 4 4 A = and B = -1 -5 4 -1 4 3 -2 3 Given the following descriptions, determine the following elementary matrices and their inverses. a. The elementary matrix E₁ multiplies the first row of A
Answers
Elementary matrix E₁ multiplies the first row of matrix A, and thus takes the form; E₁ = 1 0 0 0 1 0 0 0 1.
Given the matrices A and B, the determinant of matrix A is not equal to zero which implies that it has an inverse. Therefore, the inverse of matrix A was computed as follows; A⁻¹ = 1/(-16) (4 -2 4) (4 -2 -2) (-4 2 -2) E₁ multiplies the first row of matrix A.
Since it is an elementary matrix of the form of an identity matrix, the inverse of E₁ would be itself as it would simply undo the multiplication. Thus; E₁⁻¹ = 1 0 0 0 1 0 0 0 1.
Learn more about elementary matrix here:
https://brainly.com/question/30760739
#SPJ11
Evaluate the following integrals below. Clearly state the technique you are using and include every step to illustrate your solution. Use of functions that were not discussed in class such as hyperbolic functions will rnot get credit. (a) Why is this integral ſ3 -3 dx improper? If it converges, compute its value exactly(decimals are not acceptable) or show that it diverges.
Answers
The integral ſ3 - 3 dx is improper because it involves an unbounded interval. To determine if it converges or diverges, we need to evaluate the integral.
The given integral is ∫(-3)dx from 3 to infinity. This integral is improper because it involves an unbounded interval of integration, where the upper limit is infinity.
To evaluate the convergence or divergence of the integral, we can apply the technique of improper integration. Let's proceed with the evaluation:
∫(-3)dx = -3x
Now, we need to find the limit as x approaches infinity for the evaluated integral:
lim┬(b→∞)〖-3x〗 = lim┬(b→∞)(-3x)
As x approaches infinity, -3x also approaches negative infinity. Therefore, the limit of -3x as x approaches infinity does not exist. This indicates that the integral diverges.
Hence, the given integral ∫(-3)dx from 3 to infinity is divergent, meaning it does not have a finite value.
Learn more about integral here: https://brainly.com/question/31059545
#SPJ11
Consider the matrices
3 0 0 4 0 0 1 0 0 0 0 0
A=0 3 0 B=0 -2 0 C=0 1 0 D=0 0 0
0 0 3 0 0 5 0 0 1 0 0 0
Decide which of A, B, C, D are diagonal: A,B,C,D order, separated by commas but no spaces.)
Decide which of A, B, C, D are scalar matrices:
Answers
After considering the matrices 3 0 0 4 0 0 1 0 0 0 0 0, A=0 3 0 B=0 -2 0, C=0 1 0 D=0 0 0 ,0 0 3 0 0 5 0 0 1 0 0 0, Diagonal matrices: A, C.
Scalar matrices: A, B, C, D.
A matrix is diagonal if all its entries are equal to zero except those on the diagonal. It's also an n x n matrix that has entries in all other places but those on the diagonal. In this case, A and C are diagonal matrices. Their diagonal elements are 3, 4, and 3, 5, respectively.
On the other hand, a scalar matrix is a square matrix that has the same number in all its diagonal entries. A scalar matrix is therefore diagonal. All matrices in the given options are diagonal except matrix D. The diagonal elements of the scalar matrices are: Matrix A: 3, Matrix B: -2, Matrix C: 1, and Matrix D: 0.
To know more about matrices, visit:
https://brainly.com/question/27929071
#SPJ11
10)For positive acute angles A and B, it is known that Sin A =
35/37 and Tan B= 28/45.Find the value of cos (A+B) in simpelest
form
Answers
Given, sin A = 35/37 and tan B = 28/45.
We know that tan B = sin B / cos B
Also, sin²B + cos²B = 1
Hence, sin²B = 1 - cos²B
=> sin B / cos B = sqrt(1 - cos²B) / cos B = 28/45
Or, sin B = 28x / 45 and cos B = x / 45 (let)
Using sin²B + cos²B = 1
=> 28²x² + x² = 45²
=> x²(28² + 45²) = 45²
=> x = 45 / sqrt(28² + 45²)
Therefore, cos B = x / 45 = (45 / sqrt(28² + 45²)) / 45 = 1 / sqrt(28² + 45²)
Similarly, we can find sin A = 35 / 37 and cos A = sqrt(1 - sin²A) = 12 / 37
Now, cos(A+B) = cosAcosB - sinAsinB
Putting values of sin A, cos A, sin B and cos B in above equation, we get:
cos(A+B) = (12/37)*(1/sqrt(28²+45²)) - (35/37)*(28/45)*(1/sqrt(28²+45²))
cos(A+B) = (12*45 - 35*28) / (37*45*sqrt(28²+45²))
cos(A+B) = 501 / (37*45*sqrt(28²+45²))
Hence, the main answer is: 501 / (37*45*sqrt(28²+45²))
To know more about tan B = sin B / cos B visit:
brainly.com/question/14346186
#SPJ11
PLS HELP I NEED ANSWERS BY TMMRW
Answers
The shaded area of the figure is 86.39 square units
Calculating the area of the figureFrom the question, we have the following parameters that can be used in our computation:
The composite figure
The total area of the composite figure is the sum of the individual shapes.
In this case, we have
Quarter circle with radius 8Quarter circle with radius 5Quarter circle with radius 3Quarter circle with radius 2Semicircle with radius 2Using the above as a guide, we have the following:
Area = 1/4 * π * (8² + 5² + 3² + 2²) + 1/2 * π * 2²
Evaluate
Area = 86.39
Hence, the shaded area of the figure is 86.39 square units
Read more about area at
brainly.com/question/26403859
#SPJ1
An instructor gets 5 calls in 3 hours
a. How likely is it that the teacher will get exactly 10 calls
in 3 hours?
b. How likely is it that the student will receive 30 calls in 10
hours?
Answers
We need to make assumptions about the distribution of calls and the rate at which calls occur. First assumption is that the number of calls follows a Poisson distribution, average rate of calls is constant over time.
a. To determine the likelihood of getting exactly 10 calls in 3 hours, we need to know the average rate of calls per hour. Let's denote this rate as λ.Since the instructor receives 5 calls in 3 hours, we can calculate the average rate of calls per hour: λ = (5 calls) / (3 hours) ≈ 1.67 calls per hour. Using the Poisson distribution formula, the probability of getting exactly k calls in a given time period is given by: P(X = k) = (e^(-λ) * λ^k) / k!For k = 10 and λ = 1.67, we can calculate the probability: P(X = 10) = (e^(-1.67) * 1.67^10) / 10! b. Similarly, to determine the likelihood of receiving 30 calls in 10 hours, we need to calculate the average rate of calls per hour.
Since the student receives 5 calls in 3 hours, we can calculate the average rate of calls per hour: λ = (5 calls) / (3 hours) ≈ 1.67 calls per hour. Using the same Poisson distribution formula, we can calculate the probability for k = 30 and λ = 1.67: P(X = 30) = (e^(-1.67) * 1.67^30) / 30!
To learn more about Poisson distribution click here: brainly.com/question/30388228
#SPJ11
determine whether the value is a discrete random variable, continuous random variable, or not a random variable. the number of hits to a website in a day
Answers
The number of hits to a website in a day is a discrete random variable. In probability theory, a random variable is a variable that takes on values determined by chance. In this case, the value in question is the number of hits on a website in a day.
It can be classified as either a discrete random variable or a continuous random variable depending on the nature of the data.A discrete random variable is one that can only take on integer values, while a continuous random variable is one that can take on any value within a specified range. For example, the number of hits to a website in a day can take on any integer value from 0 to infinity. It is therefore classified as a discrete random variable.
In conclusion, the number of hits to a website in a day is a discrete random variable.
To know more about Discrete random variable visit-
brainly.com/question/17238412
#SPJ11
Let P(Z)=0.43, P(Y)=0.33, and P(ZAY)=0.16. Use a Venn diagram to find (a) P(ZOY'). (b) P(Z UY) (c) P(ZUY) and (d) P(ZnY'). (a) P(Z'NY!) - (Type an integer or a decimal)
Answers
The probability of given values: (a) P(ZOY') = 0.27 (b) P(Z U Y) = 0.60 (c) P(ZUY) = 0.60 (d) P(ZnY') = 0.10.
To find the value of P(ZOY'), we can subtract the probability of the intersection of Z and Y from the probability of Z:
P(ZOY') = P(Z) - P(Z ∩ Y)
Given that P(Z) = 0.43 and P(Z ∩ Y) = 0.16, we can substitute these values into the equation:
P(ZOY') = 0.43 - 0.16 = 0.27
Therefore, P(ZOY') is equal to 0.27.
(b) P(Z U Y) can be found by adding the probabilities of Z and Y and subtracting the probability of their intersection:
P(Z U Y) = P(Z) + P(Y) - P(Z ∩ Y)
Given that P(Z) = 0.43, P(Y) = 0.33, and P(Z ∩ Y) = 0.16, we can substitute these values into the equation:
P(Z U Y) = 0.43 + 0.33 - 0.16 = 0.60
Therefore, P(Z U Y) is equal to 0.60.
(c) P(ZUY) is the probability of the union of Z and Y, which is the same as P(Z U Y). So, P(ZUY) is also equal to 0.60.
(d) P(ZnY') represents the probability of the intersection of Z and the complement of Y. To find this value, we subtract the probability of Y from the probability of Z:
P(ZnY') = P(Z) - P(Y)
Given that P(Z) = 0.43 and P(Y) = 0.33, we can substitute these values into the equation:
P(ZnY') = 0.43 - 0.33 = 0.10
Therefore, P(ZnY') is equal to 0.10.
To know more about probability,
https://brainly.com/question/29685959
#SPJ11
10) Empty Set Facts, Also Homework. Unanswered
Ø = {0}
Select an answer and submit. For keyboard navigation, use the up/down arrow keys to select an answer.
a TRUE
b FALSE
8) Empty Set Facts Homework Unanswered
0 € 0
Select an answer and submit. For keyboard navigation, use the up/down arrow keys to select an answer.
a TRUE
b FALSE
9) Empty Set Facts, Too Homework Unanswered
{0} <Ø
Select an answer and submit. For keyboard navigation, use the up/down arrow keys to select an answer.
a TRUE
b FALSE
Answers
10) b) false
9) b) false
8) b) false
10) The statement Ø = {0} is false. The symbol Ø represents the empty set, which means it contains no elements. On the other hand, {0} is a set containing the element 0. Therefore, Ø and {0} are distinct sets, and they are not equal. The correct answer is (b) FALSE.
8) The statement 0 € 0 is false. The symbol € represents the element-of relation, indicating that an element belongs to a set. However, in this case, 0 is not an element of the empty set Ø since the empty set does not contain any elements. Therefore, 0 is not in Ø, and the statement is false. The correct answer is (b) FALSE.
9) The statement {0} < Ø is false. The symbol < represents the subset relation, indicating that one set is a proper subset of another. However, in this case, {0} is not a proper subset of the empty set Ø since {0} and Ø do not have any common elements. Therefore, {0} is not a subset of Ø, and the statement is false. The correct answer is (b) FALSE.
To learn more about navigation click here:brainly.com/question/29401885
#SPJ11
Let R be a commutative ring with unity. a) b) c) d) Write the definition of prime and irreducible elements. Write the definition of prime and maximal ideals. Jnder what conditions prime and irreducible elements are same? Justify your answers. Under what conditions prime and maximal ideals are same? Justify your answers.
Previous question
Answers
if R is a commutative ring with unity and I is a proper ideal of R, then I is maximal if and only if R/I is a field. In this case, I is also a prime ideal.
Prime and Irreducible elements:
An element p of R is called a prime element if p is not a unit and whenever p divides ab for some a,[tex]b∈R[/tex], then either p divides a or p divides b.
An element p of R is called an irreducible element if p is not a unit and whenever p=ab for some a,b∈R, then either a or b is a unit. Prime and Maximal Ideals: Let R be a commutative ring with unity. An ideal I of R is called a prime ideal if I is not R and whenever ab∈I for some a,[tex]b∈R[/tex], then either a∈I or b∈I.An ideal I of R is called a maximal ideal if I is not R and whenever J is an ideal of R with [tex]I⊆J[/tex], then either J=I or J=R.
If R is a unique factorization domain (UFD), then every irreducible element is a prime element. But if R is not a UFD, then there exist irreducible elements that are not prime elements. Thus, prime and irreducible elements are the same under UFD.
Prime ideal is always a proper ideal, but a maximal ideal is always proper and prime. Ideally, the prime ideal is a proper subset of the maximal ideal, but it is not a necessary condition that prime and maximal ideals are the same. For example, if R=Z, then the ideal (p) generated by a prime number p is a maximal ideal but not a prime ideal, while the ideal (0) is a prime ideal but not a maximal ideal.
However, if R is a commutative ring with unity and I is a proper ideal of R, then I is maximal if and only if R/I is a field. In this case, I is also a prime ideal.
To know more about commutative ring visit:
https://brainly.com/question/32227456
#SPJ11
(2) Find the divergence of a function F at the point (1,3,1) if F = x²yî + yz²ĵ + 2zk.
Answers
The divergence of F at the point (1, 3, 1) is 25.
The divergence of F is given by the formula:
div(F) = ∇ · F
where ∇ represents the gradient operator.
Given the vector function F = x²yî + yz²ĵ + 2zk, we can compute the divergence at the point (1, 3, 1) as follows:
Compute the gradient of F:
∇F = (∂/∂x, ∂/∂y, ∂/∂z) F
Taking the partial derivatives of each component of F, we get:
∂/∂x (x²y) = 2xy
∂/∂y (yz²) = z²
∂/∂z (2z) = 2
So, the gradient of F is:
∇F = (2xy)î + z²ĵ + 2k
Evaluate the gradient at the point (1, 3, 1):
∇F = (2(1)(3))î + (1)²ĵ + 2k
= 6î + ĵ + 2k
Compute the dot product of the gradient with F at the given point:
div(F) = ∇ · F = (6î + ĵ + 2k) · (x²yî + yz²ĵ + 2zk)
= (6x²y) + (yz²) + (4z)
= (6(1)²(3)) + (3(1)²(1)) + (4(1))
= 18 + 3 + 4
= 25
To learn more on Vectors click:
https://brainly.com/question/29740341
#SPJ4