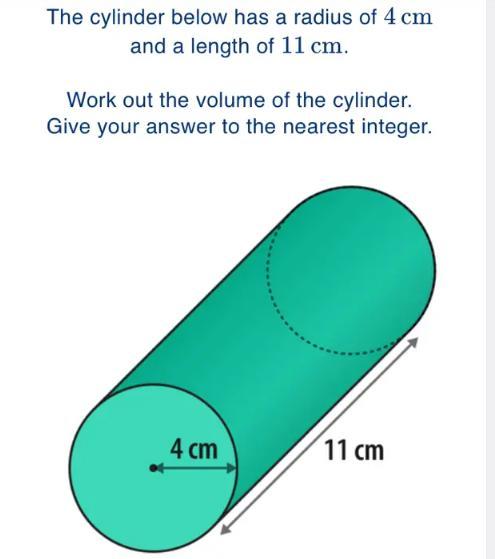
The cylinder below has a radius of 4cm and the length of 11cm

The initial velocity of the ball can be determined by finding the derivative of the height function h(t) = -4.9t² + 12t + 5 at t = 0. The impact velocity can be determined by finding the derivative of h(t) and evaluating it when the ball hits the ground (when h(t) = 0).

To determine the initial velocity of the ball, we need to find the derivative of the height function h(t) = -4.9t² + 12t + 5 with respect to t. The derivative represents the rate of change of height with respect to time, which is the velocity. Taking the

derivative

of h(t), we get h'(t) = -9.8t + 12. Evaluating h'(t) at t = 0 gives us the initial velocity.

To determine the impact velocity of the ball when it hits the ground, we need to find the time t when the height function h(t) = -4.9t² + 12t + 5 equals 0. This can be solved by setting h(t) = 0 and solving for t. Once we find the value of t, we can substitute it into the derivative h'(t) = -9.8t + 12 to obtain the

impact velocity

of the ball at that time.

To learn more about

initial velocity

brainly.com/question/28395671

#SPJ11

The nth Taylor polynomial for the function, centered at c, f(x) = ln(x), n = 4, c = 2 is T4(x) = (x - 2) - \frac{(x - 2)^2}{2} + \frac{(x - 2)^3}{3} - \frac{(x - 2)^4}{4}.

The nth Taylor polynomial for a function, f(x), centered at c is given by the formula:Tn(x) = f(c) + f'(c)(x - c) + \frac{f''(c)}{2!}(x - c)^2 + ... + \frac{f^{(n)}(c)}{n!}(x - c)^nHere, the given function is f(x) = ln(x), n = 4 and c = 2.Taking the first four derivatives, we have:f'(x) = \frac{1}{x}f''(x) = -\frac{1}{x^2}f'''(x) = \frac{2}{x^3}f^{(4)}(x) = -\frac{6}{x^4}Evaluating these at x = 2, we get:f(2) = ln(2)f'(2) = \frac{1}{2}f''(2) = -\frac{1}{8}f'''(2) = \frac{1}{8}f^{(4)}(2) = -\frac{3}{16}Substituting these values in the formula for the nth Taylor polynomial, we get:T4(x) = ln(2) + \frac{1}{2}(x - 2) - \frac{1}{2 \cdot 8}(x - 2)^2 + \frac{1}{2 \cdot 8 \cdot 8}(x - 2)^3 - \frac{3}{2 \cdot 8 \cdot 8 \cdot 2}(x - 2)^4Simplifying, we get:T4(x) = (x - 2) - \frac{(x - 2)^2}{2} + \frac{(x - 2)^3}{3} - \frac{(x - 2)^4}{4}

Know more about polynomial here:

https://brainly.com/question/11536910

#SPJ11

To eliminate the parameter t and find a simplified Cartesian equation in the form y = mx + b, the given parametric equations x(t) = 18 - t and y(t) = -13 - 3t are used. By expressing t in terms of x and substituting it into the second equation, the simplified Cartesian equation y = 3x - 67 is obtained.

The goal is to eliminate the parameter t and express the relationship between x and y in the Cartesian form y = mx + b.

Given the parametric equations x(t) = 18 - t and y(t) = -13 - 3t, we first solve the first equation for t:

t = 18 - x

Substituting this expression for t into the second equation, we have:

y = -13 - 3(18 - x)

y = -13 - 54 + 3x

y = 3x - 67

The resulting equation, y = 3x - 67, is the simplified Cartesian equation in the form y = mx + b. It represents the relationship between x and y without the parameter t. The coefficient of x, m, is 3, which represents the slope of the line, and the constant term, b, is -67, which represents the y-intercept.

To know more about Cartesian equation, click here: brainly.com/question/16920021

#SPJ11

The critical points, relative extrema and saddle points of the function are :

To find the critical points, relative extrema, and saddle points of the function f(x, y) = 4 - (x - 8)² - y², we need to compute the first and second partial derivatives with respect to x and y.

First, let's find the first-order partial derivatives:

∂f/∂x = -2(x - 8)

∂f/∂y = -2y

To find the critical points, we need to solve the system of equations:

∂f/∂x = 0

∂f/∂y = 0

Setting each partial derivative to zero, we have:

-2(x - 8) = 0 => x - 8 = 0 => x = 8

-2y = 0 => y = 0

Therefore, the only critical point is (8, 0).

Now let's compute the second-order partial derivatives:

∂²f/∂x² = -2

∂²f/∂y² = -2

∂²f/∂x∂y = 0 (Since the order of differentiation does not matter, the mixed partial derivatives are equal.)

To determine the nature of the critical point (8, 0), we need to examine the second-order partial derivatives.

The determinant of the Hessian matrix is given by:

D = (∂²f/∂x²) * (∂²f/∂y²) - (∂²f/∂x∂y)²

= (-2) * (-2) - (0)²

= 4

The value of D is positive, indicating that the critical point (8, 0) is a saddle point.

Therefore,

- The critical point is (8, 0).

- There are no relative extrema.

- The critical point (8, 0) is a saddle point.

Learn more on partial derivative :https://brainly.com/question/31280533

#SPJ4

The statement is q → r. The contrapositive of this statement is ~r → ~q. Therefore, option D. r → ~ q is the contrapositive of the given statement.

Let's understand the contrapositive of the given statement. A contrapositive of a statement is when you negate both the hypothesis and the conclusion of a conditional statement and then switch their order. In other words, you can form the contrapositive of a statement "if p, then q" as follows:

If ~q, then ~p.

Now that we understand what is a contrapositive of the statement, let's move on to solving this.  The given statement is q → r, The contrapositive of this statement is ~r → ~q. Therefore, option D. r → ~ q is the contrapositive of the given statement. So, the answer is D. r → ~ q.

You can learn more about contrapositive at: brainly.com/question/12151500

#SPJ11

(A) The value of sin(φ)  and cos(φ)  when φ ≈ 0 are φ and 1 respectively

(B) By substituting the approximations for sin and cos, the approximate solution is φ + 3b = 0

(C) By solving for φ, the value of φ = -3b

(A) To estimate the values of sin(φ) and cos(φ) when φ ≈ 0 using derivatives and the linear approximation, we can use the first-order Taylor series expansion of sine and cosine functions.

The linear approximation of a function f(x) near a point x = a is given by:

f(x) = f(a) + f'(a)(x - a)

Let's apply this approximation to the sine and cosine functions when φ ≈ 0:

For sine:

sin(φ) ≈ sin(0) + cos(0)(φ - 0)

        ≈ 0 + 1(φ - 0)

        ≈ φ

For cosine:

cos(φ) ≈ cos(0) - sin(0)(φ - 0)

        ≈ 1 - 0(φ - 0)

        ≈ 1

Therefore, when φ ≈ 0, sin(φ) ≈ φ and cos(φ) ≈ 1.

(B) Now, let's approximate the given equation by substituting the approximations for sin(φ) and cos(φ).

Original equation: sin(φ) + b(1 + cos²(φ) + cos(φ)) = 0

Substituting the approximations:

φ + b(1 + 1² + 1) = 0

φ + 3b = 0

(C) To solve for φ approximately, we can rearrange the equation:

φ = -3b

Therefore, the approximate solution for φ is φ ≈ -3b.

Learn more about phase angle here:

https://brainly.com/question/31114195

#SPJ4

The rate of production of the new cell phone is given by the function P(t) = 50(2t + 150), where t represents the number of days. To calculate the total number of telephones produced during the first 3 months (90 days), we need to find the integral of the production rate function over the given time interval.

The rate of production of the telephone is represented by the function P(t) = 50(2t + 150), where t is the number of days. This function gives us the number of units produced per day. To find the total number of telephones produced during the first 3 months (90 days), we need to calculate the integral of the production rate function over the interval [0, 90].

Using integral calculus, we can evaluate the integral ∫P(t) dt from 0 to 90 to find the total number of telephones produced during the given time period. By substituting the limits of integration and evaluating the integral, we can determine the final result.

It is important to note that the production rate function is linear, meaning the rate of production increases linearly with time. By integrating the function over the specified time interval, we can find the cumulative number of telephones produced during the first 3 months (90 days).

To learn more about integral, click here:

brainly.com/question/31059545

#SPJ11

To determine the number of ways of filling the position of Class President with 4 candidates and the position of Class Vice-President with 3 candidates, we can use the concept of permutations. The number of ways to fill the Class President position is given by the number of permutations of 4 candidates, which is 4! (4 factorial).

Similarly, the number of ways to fill the Class Vice-President position is given by the number of permutations of 3 candidates, which is 3! (3 factorial). Therefore, there are 4! = 24 ways to fill the position of Class President and 3! = 6 ways to fill the position of Class Vice-President.

To calculate the number of ways of filling the position of Class President with 4 candidates, we use the concept of permutations. Since there are 4 candidates, we have 4 options for the first position, 3 options for the second position, 2 options for the third position, and 1 option for the last position. Therefore, the number of ways to fill the Class President position is given by 4! (read as "4 factorial"), which is equal to 4 * 3 * 2 * 1 = 24.

Similarly, to determine the number of ways of filling the position of Class Vice-President with 3 candidates, we have 3 options for the first position, 2 options for the second position, and 1 option for the last position. Thus, the number of ways to fill the Class Vice-President position is given by 3!, which is equal to 3 * 2 * 1 = 6.

to learn more about concept of permutations click here; brainly.com/question/32683496

#SPJ11

The number of goals scored by individual players on a hockey team represents an example of a discrete variable.

In the context of hockey, a discrete variable refers to a characteristic that can only take specific, separate values. The number of goals scored by players on a hockey team is an example of a discrete variable. Each player can score a certain number of goals, and these values are distinct and separate from one another. It is not possible to have fractional or continuous values for the number of goals scored.

Each goal scored is counted as a whole number, making it a discrete variable. Discrete variables, such as the number of goals scored by players in a hockey team, are distinct and separate values that do not fall on a continuum. They are typically counted or enumerated and can only take specific values without any intermediate values between them.

This is in contrast to continuous variables, which can take any value within a given range. Understanding the difference between discrete and continuous variables is essential in various fields, including statistics, mathematics, and data analysis.

Learn more about discrete variable

brainly.com/question/19338975

#SPJ11

The minimum cost while still meeting building code is achieved by using 150 Sitka spruce planks and 225 basswood planks.

Let the number of large cabinets be x and the number of small cabinets be y.The objective function is [tex]P(x,y) = 70x + 58y.[/tex]

The constraint equation is [tex]50x + 30y ≤ 450.[/tex]

Graph the feasible region and determine the vertices as follows:

[tex]vertex 1: (0, 15)vertex 2: (9, 12)\\vertex 3: (18, 6)\\vertex 4: (9, 0)[/tex]

Then test the objective function at each vertex.

[tex]P(0,15) = 70(0) + 58(15) \\= 870P(9,12) \\= 70(9) + 58(12) \\= 1236P(18,6) \\= 70(18) + 58(6) \\= 1560P(9,0) \\= 70(9) + 58(0) \\= 630[/tex]

Hence, the company should manufacture 18 small cabinets and 6 large cabinets to maximize its income.2) You are a civil engineer designing a bridge.

The walkway needs to be made of wooden planks.

You are able to use either Sitka spruce planks (which weigh 3 pounds each), basswood planks (which weigh 4 pounds each), or a combination of both.

The total weight of the planks must be between 600 and 900 pounds to meet the safety code. If Sitka spruce planks cost $3.

25 each and basswood planks cost $3.75 each, how many of each plank should you use to minimize cost while still meeting the building code?

Let x be the number of Sitka spruce planks and y be the number of basswood planks.

Each Sitka spruce plank weighs 3 pounds while each basswood plank weighs 4 pounds.

Thus, the objective function is [tex]C(x,y) = 3.25x + 3.75y.[/tex]

The constraint equations are: [tex]x + y ≥ 1500x ≥ 0y ≥ 0[/tex]

The total weight of the planks must be between 600 and 900 pounds in order to meet the safety code.

Therefore, [tex]3x + 4y ≥ 6003x + 4y ≤ 900[/tex]

Graph the feasible region and determine the vertices as follows:

[tex]vertex 1: (0, 375)\\vertex 2: (0, 150)\\vertex 3: (150, 225)\\vertex 4: (225, 125)vertex 5: (300, 0)[/tex]

Then test the objective function at each vertex.

[tex]C(0,375) = 3.25(0) + 3.75(375) \\= 1406.25C(0,150) \\= 3.25(0) + 3.75(150) \\= 562.5C(150,225) \\= 3.25(150) + 3.75(225) \\= 1312.5C(225,125) \\= 3.25(225) + 3.75(125) \\= 1462.5C(300,0) \\= 3.25(300) + 3.75(0) \\=975[/tex]

Therefore, the minimum cost while still meeting the building code is achieved by using 150 Sitka spruce planks and 225 basswood planks.

Know more about costs here:

https://brainly.com/question/29509552

#SPJ11

The statement [tex]L{t f(t)} = (-1)^n * d^n {L[f(t)]} / ds^n[/tex], where L{ } represents the Laplace transform and d/ds denotes differentiation with respect to s, is proven to be true using the Principle of Mathematical Induction.

To prove the statement using the Principle of Mathematical Induction, we need to follow these steps:

Simplifying the right side of the equation, we have:

L{t f(t)} = 1 * L[f(t)]

This matches the left side of the equation, so the statement holds true for the base case.

This is our inductive hypothesis.

We need to prove that if the statement is true for n = k, then it is also true for n = k + 1.

Using the properties of differentiation and linearity of the Laplace transform, we can rewrite the equation as:

[tex]L{f(t)} = (-1)^k * d^{(k+1)} {L[f(t)]} / ds^{(k+1)}[/tex]

This matches the form of the statement for n = k + 1, so the statement holds true for the inductive step.

By the Principle of Mathematical Induction, the statement is true for all positive integers n. Therefore, we have proven that:

[tex]L{t f(t)} = (-1)^n * d^n {L[f(t)]} / ds^n[/tex] for all positive integers n.

To know more about Mathematical Induction,

https://brainly.com/question/30711158

#SPJ11

The  values are x₀ = 1, x₁ = 8, x₂ = 46, y₀ = 2, y₁ = 10, and y₂ = 62.

Given system of equations:

x₍ₙ₊₁₎ = 2xₙ + 3yₙ     (1)

y₍ₙ₊₁₎ = 4xₙ + 3yₙ     (2)

Initial values:

x₀ = 1

y₀ = 2

To solve the system, we need to find expressions for xₙ and yₙ in terms of n.

1. Solving equation (1):

From equation (1), we have:

x₍ₙ₊₁₎ = 2xₙ + 3yₙ

Substituting n = 0:

x₁ = 2x₀ + 3y₀

   = 2(1) + 3(2)

   = 2 + 6

   = 8

Substituting n = 1:

x₂ = 2x₁ + 3y₁

   = 2(8) + 3y₁

2. Solving equation (2):

From equation (2), we have:

y₍ₙ₊₁₎ = 4xₙ + 3yₙ

Substituting n = 0:

y₁ = 4x₀ + 3y₀

   = 4(1) + 3(2)

   = 4 + 6

   = 10

Substituting n = 1:

y₂ = 4x₁ + 3y₁

   = 4(8) + 3(10)

   = 32 + 30

   = 62

So, the solution to the system of difference equations is:

x₀ = 1

x₁ = 8

x₂ = 2(8) + 3y₁ = 16 + 3y₁

y₀ = 2

y₁ = 10

y₂ = 4(8) + 3(10) = 32 + 30 = 62

The expressions for x₂ and y₂ depend on the value of y₁, which can be determined using the given equations or by substituting the values obtained for x and y in the subsequent equations.

To learn more about differential equation: https://brainly.com/question/1164377

#SPJ11

The final answer in terms of constants [tex]y(t) = -e^t - e^{(-2t)} - (11/6)e^{(-t)}sin(3t)[/tex]

What is the exponential function?

An exponential function is a mathematical function of the form:

f(x) = aˣ

where "a" is a constant called the base, and "x" is a variable. Exponential functions can be defined for any base "a", but the most common base is the mathematical constant "e" (approximately 2.71828), known as the natural exponential function.

Step 1: Taking the Laplace transform of the given differential equation:

Apply the Laplace transform to each term and use the linearity property:

L{y''} + L{y'} - 2L{y} = L{3cos(3t)} - 11L{sin(3t)}

Using the derivative property and the Laplace transform of trigonometric functions, we have:

s²Y(s) - sy(0) - y'(0) + sY(s) - y(0) - 2Y(s) = 3 * (s / (s² + 9)) - 11 * (3 / (s² + 9))

Step 2: Applying the initial conditions:

Substitute y(0) = 0 and y'(0) = 6 into the transformed equation:

s²Y(s) - 6s - 6 + sY(s) - 0 - 2Y(s) = 3 * (s / (s² + 9)) - 11 * (3 / (s² + 9))

Simplifying:

s²Y(s) + sY(s) - 2Y(s) - 6s = 3s / (s² + 9) - 33 / (s² + 9) - 6

Step 3: Solving for Y(s):

Combine like terms:

Y(s) * (s² + s - 2) = (3s - 33) / (s² + 9) - 6s + 6

Divide both sides by (s² + s - 2):

Y(s) = [(3s - 33) / (s² + 9) - 6s + 6] / (s² + s - 2)

Step 4: Use inverse Laplace transform:

To find the solution in the time domain, we need to find the inverse Laplace transform of Y(s). This involves decomposing the right side into partial fractions.

The denominator s² + s - 2 can be factored as (s - 1)(s + 2), so we can rewrite Y(s) as:

Y(s) = [(3s - 33) / (s² + 9) - 6s + 6] / [(s - 1)(s + 2)]

Using partial fraction decomposition, we can write:

Y(s) = A / (s - 1) + B / (s + 2) + C(s - 1)(s + 2) / (s² + 9)

Now, we need to find the values of A, B, and C. We can do this by equating the numerators:

(3s - 33) = A(s + 2)(s² + 9) + B(s - 1)(s² + 9) + C(s - 1)(s + 2)

To find A, we set s = 1:

3(1) - 33 = A(1 + 2)(1² + 9) + B(1

- 1)(1² + 9) + C(1 - 1)(1 + 2)

-30 = 30A

A = -1

To find B, we set s = -2:

3(-2) - 33 = A(-2 + 2)(-2² + 9) + B(-2 - 1)(-2² + 9) + C(-2 - 1)(-2 + 2)

-39 = 39B

B = -1

Now, we have A = -1 and B = -1. To find C, we can choose any other value for s, for example, s = 0:

3(0) - 33 = A(0 + 2)(0² + 9) + B(0 - 1)(0² + 9) + C(0 - 1)(0 + 2)

-33 = 18C

C = -33/18 = -11/6

Now we can rewrite Y(s) as:

Y(s) = -1 / (s - 1) - 1 / (s + 2) - (11/6)(s - 1)(s + 2) / (s² + 9)

Taking the inverse Laplace transform, we obtain the solution in the time domain:

[tex]y(t) = -e^t - e^{(-2t)} - (11/6)e^{(-t)}sin(3t)[/tex]

Hence, the final answer in terms of constants [tex]y(t) = -e^t - e^{(-2t)} - (11/6)e^{(-t)}sin(3t)[/tex]

To learn more about the exponential function visit:

https://brainly.com/question/30241796

#SPJ4

We can be 90% confident that the true population mean μ lies between $62,619.98 and $67,780.02.

A confidence interval for the population mean μ can be constructed using the formula x ± z*(σ/√n), where

x is the sample mean,

z* is the critical value

σ is the population standard deviation

n is the sample size.

In this case, the sample mean x is $65,200, the population standard deviation σ is $16,009, and the sample size n is 50.

For a 90% confidence level, the critical value z* is 1.645

Substituting these values into the formula above, we get a 90% confidence interval for the population mean μ of

$65,200 ± 1.645*($16,009/√50)

= ($62,619.98, $67,780.02).

So we can be 90% confident that the true population mean μ lies between $62,619.98 and $67,780.02.

Read more on true population mean herehttps://brainly.com/question/31358131

#SPJ4

To obtain a 95% confidence interval for the mean monthly income with a margin of error of $20, a sample size of 95 students should be selected.

To determine the required sample size, we need to consider the population standard deviation, desired confidence level, and the desired margin of error.

In this case, the population standard deviation is given as $110, and the desired margin of error is $20. The desired confidence level is 95%, which corresponds to a z-score of 1.96 for a two-tailed test.

Using the formula for the sample size calculation for estimating the mean, which is n = (z² * σ²) / E², where z is the z-score, σ is the population standard deviation, and E is the margin of error, we can substitute the given values and solve for the sample size.

Plugging in the values, we have n = (1.96^2 * 110²) / 20², which simplifies to n ≈ 93.14.

Since we cannot have a fraction of a student, we round up to the nearest whole number. Therefore, a sample size of 95 students should be selected.

Learn more about standard deviation

brainly.com/question/13498201

#SPJ11

To check the convergence of the series using the Integral Test, we need to verify the necessary conditions.

The series in question is:

∑ [sin²(2 + n²) + cos²(2)]

We can rewrite the series as:

∑ [1]

Since sin²(2 + n²) + cos²(2) simplifies to 1 for all terms, the series becomes an infinite geometric series with a common ratio of 1.

The conditions of the Integral Test are:

The terms of the series are positive.

The terms of the series are decreasing.

The integral of the terms of the series is finite.

Let's verify these conditions:

The terms of the series, which are all equal to 1, are positive.

To check if the terms are decreasing, we compare consecutive terms:

1 ≥ 1

The terms are not strictly decreasing, but they are constant. Therefore, the terms are not increasing either. So, we can say the terms are non-increasing.

We need to evaluate the integral of the terms to check if it is finite:

∫ [1] dn

Integrating 1 with respect to n gives us n + C, where C is the constant of integration.

The integral is not finite as it grows without bound. Thus, the integral of the terms is not finite.

Since the third condition of the Integral Test is not satisfied, we cannot conclude anything about the convergence of the series using this test.

In this case, we cannot determine the convergence or divergence of the series using the Integral Test. Other convergence tests, such as the Comparison Test or the Ratio Test, may be more suitable for analyzing this series.

To learn more about integration : brainly.com/question/31744185

#SPJ11

Domain: All positive real numbers. Range: All real numbers. the transformed exponential function is wider than the standard exponential function f(x) = ex.

Step by step answer:

Transformation of the graph f(x) = -3 + 2e^(x-2) from

f(x) = ex1.

Vertical shift: The first transformation that can be observed is the vertical shift downwards by 3 units. The standard exponential function f(x) = ex passes through the point (0,1), and the transformed exponential function f(x) = -3 + 2e^(x-2) passes through the point (2,-1).

2. Horizontal shift: The second transformation is the horizontal shift rightwards by 2 units. The standard exponential function f(x) = ex has an asymptote at

y=0 and passes through the point (1,e), while the transformed exponential function f(x) = -3 + 2e^(x-2) has an asymptote at

y=-3 and passes through the point (3,1).

3. Vertical stretch/compression: The third transformation is the vertical stretch by a factor of 2. The standard exponential function f(x) = ex passes through the point (1,e) and has the range (0,∞), while the transformed exponential function f(x) = -3 + 2e^(x-2) passes through the point (3,1) and has the range (-3,∞). The vertical stretch by a factor of 2, stretches the vertical range of the transformed exponential function f(x) = -3 + 2e^(x-2) to (-6,∞). Therefore, the transformed exponential function is wider than the standard exponential function f(x) = ex.

To know more about Domain visit :

https://brainly.com/question/30133157

#SPJ11

Yes, there is significant variation in climate denialism across political parties.

There is indeed significant variation in climate denialism across different political parties. Numerous studies have consistently demonstrated that certain political parties exhibit higher levels of skepticism or denial regarding the scientific consensus on climate change.

In particular, conservative Republicans tend to express higher levels of climate denialism compared to Democrats. This variation in attitudes towards climate change can be influenced by factors such as interest groups, ideological beliefs, and media narratives.

It is important to note that while these trends exist on a party level, they do not necessarily reflect the views of every individual within a specific political party.

Learn more about variation

brainly.com/question/29773899

#SPJ11

The probability of getting 16 or more successes in this binomial experiment is approximately 0.272.

The mean (expected value) of this binomial experiment is 14.4.

Part 1 of 3:

(a) To determine the probability P(16 or more) in a binomial experiment with n = 18 trials and success probability p = 0.8,

we need to calculate the probability of getting 16, 17, or 18 successes.

We can use the binomial probability formula or a binomial probability calculator to calculate the probabilities for each individual outcome and then add them together:

P(16 or more) = P(X = 16) + P(X = 17) + P(X = 18)

Using the binomial probability formula

P(X = k) = (n C k) × [tex]p^k[/tex] × [tex](1 - p)^{(n - k)}[/tex],

where (n C k) represents the number of combinations of n items taken k at a time, we can calculate the probabilities:

P(16 or more) = (18 C 16) × 0.8¹⁶ × (1 - 0.8)⁽¹⁸⁻¹⁶⁾ + (18 C 17) × 0.8¹⁷ × (1 - 0.8)⁽¹⁸⁻¹⁷⁾ + (18 C 18) * 0.8¹⁸ × (1 - 0.8)⁽¹⁸⁻¹⁸⁾

Calculating these values, we find:

P(16 or more) ≈ 0.272

So, the probability of getting 16 or more successes in this binomial experiment is approximately 0.272.

Part 2 of 3:

(b) To find the mean (expected value) of a binomial distribution, we can use the formula:

Mean (μ) = n × p

Plugging in the given values n = 18 and p = 0.8, we can calculate the mean:

Mean (μ) = 18 × 0.8

Mean (μ) = 14.4

So, the mean (expected value) of this binomial experiment is 14.4.

To learn more about binomial experiment, visit:

https://brainly.com/question/30888365

#SPJ11

The correct answers are:

(a) The operator [tex]\(\psi\)[/tex] is a normal operator if and only if [tex]\(\psi\)[/tex] commutes with its adjoint [tex]\(\psi^*\)[/tex]. Let [tex]\(\beta\)[/tex] be an ordered orthonormal basis of [tex]\(V\)[/tex]. Then, the matrix representation of [tex]\(\psi\)[/tex] with respect to [tex]\(\beta\)[/tex] is [tex]([\psi]_{\beta}\)[/tex]. The adjoint of [tex]\(\psi\)[/tex] is [tex](\psi^*\ )[/tex], and the matrix representation of [tex]\(\psi^*\)[/tex] with respect to [tex]\(\beta\)[/tex] is [tex]\([\psi^*]_{\beta}\)[/tex]. Therefore, [tex]\(\psi\)[/tex] is a normal operator if and only if [tex]([\psi]_{\beta}\)[/tex] commutes with [tex]\([\psi^*]_{\beta}\)[/tex], which means [tex]\([\psi]_{\beta}\)[/tex] is a normal matrix.

(b) The operator [tex]\(\psi\)[/tex] is a unitary operator if and only if [tex]\(\psi\)[/tex] is invertible and [tex]\(\psi^{-1} = \psi^*\)[/tex]. Let [tex]\(\beta\)[/tex] be an ordered orthonormal basis of [tex]\(V\)[/tex]. The matrix representation of [tex]\(\psi\)[/tex] with respect to [tex]\(\beta\) is \([\psi]_{\beta}\)[/tex]. The adjoint of [tex]\(\psi\)[/tex] is \[tex](\psi^*\ )[/tex], and the matrix representation of [tex]\(\psi^*\)[/tex] with respect to [tex]\(\beta\)[/tex] is [tex]\([\psi^*]_{\beta}\)[/tex]. Therefore, [tex]\(\psi\)[/tex] is a unitary operator if and only if [tex]([\psi]_{\beta}\)[/tex] is invertible and [tex]\([\psi]_{\beta}^{-1} = [\psi^*]_{\beta}\)[/tex], which means [tex]\([\psi]_{\beta^*\theta}\)[/tex] is a unitary matrix.

(c) The operator [tex]\(\psi\)[/tex] is self-adjoint if and only if [tex]\(\psi = \psi^*\)[/tex]. Let [tex]\(\beta\)[/tex] be an ordered orthonormal basis of [tex]\(V\)[/tex]. The matrix representation of [tex]\(\psi\)[/tex] with respect to [tex]\(\beta\)[/tex] is [tex]\([\psi]_{\beta}\)[/tex]. The adjoint of [tex]\(\psi\)[/tex] is [tex]\(\psi^*\),[/tex] and the matrix representation of \[tex](\psi^*\ )[/tex] with respect to [tex]\(\beta\) is \([\psi^*]_{\beta}\)[/tex]. Therefore, [tex]\(\psi\)[/tex] is self-adjoint if and only if [tex]\([\psi]_{\beta} = [\psi^*]_{\beta}\)[/tex], which means \[tex]([\psi^2]_{\beta}\)[/tex] is self-adjoint.

(d) The operator [tex]\(\psi\)[/tex] is skew self-adjoint if and only if [tex]\(\psi = -\psi^*\). Let \(\beta\)[/tex] be an ordered orthonormal basis of [tex]V[/tex]. The matrix representation of [tex]\(\psi\)[/tex] with respect to [tex]\(\beta\)[/tex] is [tex]\([\psi]_{\beta}\)[/tex]. The adjoint of [tex]\(\psi\)[/tex] is [tex]\(\psi^*\)[/tex], and the matrix representation of [tex]\(\psi^*\)[/tex] with respect to [tex]\(\beta\)[/tex] is [tex]\([\psi^*]_{\beta}\)[/tex]. Therefore, [tex]\(\psi\)[/tex] is skew self-adjoint if and only if [tex]\([\psi]_{\beta} = -[\psi^*]_{\beta}\)[/tex], which means [tex]\([\psi]_{\beta}\)[/tex] is skew self-adjoint.

Hence, the answers are:

NOTE: The given question is incomplete. The complete question is:

Let [tex]\(V\)[/tex] be a finite-dimensional inner product space over [tex]\(F\)[/tex]. Let [tex]\(\psi\)[/tex] in[tex](\mathcal{L}(V)\) and \(\beta\)[/tex] be an ordered orthonormal basis of [tex]V[/tex]. Show that:

(a) [tex]\(\psi\)[/tex] is a normal operator if and only if [tex]\([\psi]_{\beta}\)[/tex] is a normal matrix.

(b) [tex]\(\psi\)[/tex] is a unitary operator if and only if [tex]\([\psi]_{\beta^*\theta}\)[/tex] is a unitary matrix.

(c) [tex]\(\psi\)[/tex] is self-adjoint if and only if [tex]\([\psi^2]_{\beta}\)[/tex] is self-adjoint.

(d) [tex]\(\psi\)[/tex] is skew self-adjoint if and only if [tex]\([\psi]_{\beta}\)[/tex] is skew self-adjoint.

For more such questions on unitary matrix:

https://brainly.com/question/29806169

#SPJ8

The power output of the battery is given by the function P = -(r + 0.5)², where 'r' represents the resistance in the circuit. To determine whether the power is at a maximum, we need to find the value of 'r' that maximizes the power function.

To find this value, we take the derivative of the power function with respect to 'r'. The derivative of P with respect to 'r' is dP/dr = -2(r + 0.5). Setting this derivative equal to zero, we have -2(r + 0.5) = 0. Solving for 'r', we find r = -0.5. Therefore, the resistance value that maximizes the power output of the battery is -0.5. When the resistance is equal to -0.5, the power function reaches its maximum value. This means that for any other resistance value, the power output will be lower than the maximum value attained at r = -0.5.

In conclusion, the power output of the battery is maximized when the resistance in the circuit is equal to -0.5.

Learn more about derivative here: brainly.com/question/29144258

#SPJ11

(a) The variance and standard deviation of the data set can be calculated using the given formulae.

(b) Subtracting the mean from every observation would not change the variance, but the standard deviation would remain the same.

(c) Dividing each observation by the standard deviation (standardization) would result in a variance of 1 and a standard deviation of 1.

(a) To calculate the variance, we need to find the average of the squared differences between each observation and the mean. The standard deviation is the square root of the variance. By using the given formulae, we can compute both values.

(b) When we subtract the mean from every observation, the new mean becomes 0 because the sum of the differences is zero. The variance is not affected by the shift in mean because it is calculated using the squared differences from the mean. Therefore, the variance remains the same. The standard deviation, being the square root of the variance, also remains the same.

(c) After dividing each observation by the standard deviation, the new variance becomes 1, and the new standard deviation becomes 1 as well. This happens because dividing each observation by the standard deviation scales the data such that the standard deviation becomes 1. Consequently, the variance, which is calculated based on the squared differences, also becomes 1.

Learn more about deviation:

brainly.com/question/31835352

#SPJ11

We are given that the inverse of the matrix [tex]`0 0 0 i a i b d i` is `0 0 0 i p i q r i`[/tex]. We need to find `p, q`, and `r` in terms of `a, b`, and `d`. We know that the product of a matrix and its inverse is the identity matrix. Therefore, we have[tex](0 0 0 i a i b d i ) (0 0 0 i p i q r i) =  I[/tex] where I is the identity matrix, which is[tex]`1 0 0 0 1 0 0 0 1`.[/tex]

Multiplying the matrices, we get [tex]`0 0 0 + i(p)(a) + i(q)(b) + i(r)(d) = 1`[/tex] This implies that [tex]`pa + qb + rd = 0`.[/tex] Also, all the other entries of the identity matrix should be zero. We have 4 more equations to solve for `p, q`, and `r`. They are: [tex]`ai + 0 + 0 + 0 = 0`[/tex](First column of the identity matrix)`.

Substituting the values of `p, q`, and `r`, we get  :[tex]`a(-a/d) + b(-b/d) + d(-1)\\ = 1``-a^2/d - b^2/d - d\\ = 1``-a^2 - b^2 - d^2 \\= d``d^2 + a^2 + b^2 \\= 1`[/tex]

Therefore, the values of `p, q`, and `r` in terms of `a, b`, and `d` are[tex]:`p = -a/d``q \\= -b/d``r\\ = -1`.[/tex]

To know more about inverse visit:

https://brainly.com/question/30339780

#SPJ11

Overfitting is the reason the loss function during a training process keeps decreasing for the training set. The Option A.

This scenario suggests that the model is overfitting the training set. Overfitting occurs when a model learns the specific patterns and noise in the training data to a high degree, but fails to generalize well to unseen data.

As a result, the model may perform well on the training set, leading to a decreasing loss function but it fails to capture the underlying patterns in the testing set, resulting in a stagnant or increasing loss. This could be due to the model being too complex, having too many parameters, or not being regularized effectively to prevent overfitting.

Read more about training set

brainly.com/question/29382846

#SPJ4

The flow magnitude corresponding to a 50-yr return period is 80000 cfs, the return period for a flow magnitude of 50,000 cfs is 4 years, the probability that the flow exceeds 20,000 cfs is 0.71 and the probability that the flow falls between 20,000 cfs and 50,000 cfs is 0.67.

d) The probability that the flow falls between 20,000 cfs and 50,000 cfs:

The probability is found by subtracting the probability of the flow exceeding 50,000 cfs from the probability of the flow exceeding 20,000 cfs.

So, the probability of the flow exceeding 50,000 cfs is 0.04 and the probability of the flow exceeding 20,000 cfs is 0.71.

Hence, the probability that the flow falls between 20,000 cfs and 50,000 cfs is (0.71 - 0.04) = 0.67.

The flow magnitude corresponding to a 50-yr return period is 80000 cfs, the return period for a flow magnitude of 50,000 cfs is 4 years, the probability that the flow exceeds 20,000 cfs is 0.71 and the probability that the flow falls between 20,000 cfs and 50,000 cfs is 0.67.

Know more about magnitude here:

https://brainly.com/question/24468862

#SPJ11

The correct option is  c.The formula for calculating the degrees of freedom for the pooled t-test is as follows:

df = (n1 - 1) + (n2 - 1) Where

n1 is the sample size of the first sample and n2 is the sample size of the second sample.

Using the given information, we have:

n1 = 26, n2 = 15

Substituting these values into the formula, we get:

df = (26 - 1) + (15 - 1)

df = 25 + 14

df = 39

Therefore, the number of degrees of freedom for the pooled t-test is 39. The correct option is letter c.

To know more about Degrees of freedom visit-

brainly.com/question/32093315

#SPJ11

The triangles WUV and RUW are similar by the SAS similarity statement

From the question, we have the following parameters that can be used in our computation:

The triangles in this figure are

WUV and RUW

These triangles are similar is because:

The triangles have similar corresponding sides and congruent angles

By definition, the SAS similarity statement states that

"If two sides in one triangle are proportional to two sides in another triangle and the included angle in both are congruent, then the two triangles are similar"

This means that they are similar by the SAS similarity statement

Read mroe about similar triangles at

brainly.com/question/31898026

#SPJ1

f(-2) = -55.

To evaluate f(-2) using the Remainder Theorem, we substitute x = -2 into the function f(x) = 3x^5 + 5x^2 - 4x^3 + 7x + 3 and find the remainder.

f(x) = 3x^5 + 5x^2 - 4x^3 + 7x + 3

Substituting x = -2:

f(-2) = 3(-2)^5 + 5(-2)^2 - 4(-2)^3 + 7(-2) + 3

Calculating this expression will give us the value of f(-2). Let's perform the calculations:

f(-2) = 3(-32) + 5(4) - 4(-8) - 14 + 3

f(-2) = -96 + 20 + 32 - 14 + 3

f(-2) = -55

Therefore, f(-2) = -55.

The Remainder Theorem states that if a polynomial f(x) is divided by x - a, then the remainder is equal to f(a).

In this case, we have the function f(x) = 3x^5 + 5x^2 - 4x^3 + 7x + 3 and we want to find f(-2).

To evaluate f(-2) using the Remainder Theorem, we substitute x = -2 into the function:

f(-2) = 3(-2)^5 + 5(-2)^2 - 4(-2)^3 + 7(-2) + 3

Calculating the expression will give us the value of f(-2):

f(-2) = 3(-32) + 5(4) - 4(-8) - 14 + 3

f(-2) = -96 + 20 + 32 - 14 + 3

f(-2) = -55

Therefore, according to the Remainder Theorem, f(-2) = -55.

Visit here to learn more about Remainder Theorem brainly.com/question/30242664

#SPJ11

The set is not a basis for R² because there is a scalar of -4 that gives the second vector when multiplied by the first vector. This implies that the two vectors are linearly dependent, and so they can't span the R² plane. Therefore, option (b) {(4, 1), (-7.-8)} is the correct answer..

(a) {(3, 1). (0, 0)} : The set is not a basis for R² because it has only two vectors and the second vector is the zero vector. So, we can't form a basis for R² with these vectors.

(b) {(4, 1), (-7.-8)} : The set is a basis for R² because the two vectors are linearly independent and span the entire R² plane.

(c) {(5.2).(-1,3)} :The set is not a basis for R² because there is a scalar of 5.2 which is not an integer.

This implies that the two vectors are linearly dependent, and so they can't span the R² plane.

(d) {(3,9). (-4.-12)} : The set is not a basis for R² because there is a scalar of -4 that gives the second vector when multiplied by the first vector.

This implies that the two vectors are linearly dependent, and so they can't span the R² plane.

The answer is (b) {(4, 1), (-7.-8)}. Two vectors form a basis of R² if they are linearly independent and span R².

Let's check:(a) {(3, 1). (0, 0)}: It's not a basis for R² because it has only two vectors, and the second vector is the zero vector. Therefore, we can't form a basis for R² with these vectors.

(b) {(4, 1), (-7.-8)}: This set is a basis for R² because the two vectors are linearly independent and span the entire R² plane.

To see that the vectors are linearly independent, let's suppose that there exist constants a, b such that: 4a - 7b

= 0 1a - 8b

= 0.

This is a system of two equations in two unknowns. The augmented matrix of this system is: 4 -7 | 0 1 -8 | 0.

By performing the elementary row operations R₂ -> R₂ + 7R₁, we get: 4 -7 | 0 0 -49 | 0. By performing the elementary row operations R₂ -> -R₂/49, we get: 4 -7 | 0 0 1 | 0

This system has a unique solution, which is a = 7/49 and b = 4/49. This implies that the vectors (4, 1) and (-7, -8) are linearly independent and can span R². Therefore, they form a basis for R².

(c) {(5.2).(-1,3)}: The set is not a basis for R² because there is a scalar of 5.2 which is not an integer. This implies that the two vectors are linearly dependent, and so they can't span the R² plane.

We can check this by computing the determinant of the matrix formed by these vectors: |-1 3| 5.2 15.6.

This determinant is zero, which implies that the two vectors are linearly dependent.

(d) {(3,9). (-4.-12)}: The set is not a basis for R² because there is a scalar of -4 that gives the second vector when multiplied by the first vector.

This implies that the two vectors are linearly dependent, and so they can't span the R² plane.

Therefore, the answer is (b) {(4, 1), (-7.-8)}.

To know more about vector, refer

https://brainly.com/question/28028700

#SPJ11

The statement is false. If Fx(a) = 1, it does not imply that Fx(b) = 1 for all values of b (b > a).

The statement is true. The probability mass function of a discrete random variable X, pX(x), always satisfies 0 ≤ pX(x) ≤ 1, regardless of the value of x.

The statement falsely claims that if Fx(a) = 1, then Fx(b) = 1 for all b > a in the cumulative distribution function (CDF) of a random variable X. However, the CDF can increase in steps and may not reach 1 for all values beyond a. Thus, the correct answer is B. False.
The probability mass function (PMF), pX(-), provides the probability for a discrete random variable X taking on a specific value. The statement is true, as 0 ≤ pX(x) ≤ 1 always holds for any value of x. Probabilities are bounded between 0 and 1, so the probability for any value that X can take will fall within this range. Thus, the correct answer is A. True.

Learn more about CDF here:
brainly.com/question/30402457

#SPJ11