HELP US! A middle school dance team held a carwash and recorded the following donations received during the first two hours. $25, $32, $35, $10, $18, $48, $45, $20, $15, $12
Part A: Describe the five-number summary of the data set. Then explain what each value represents in the context of the problem.


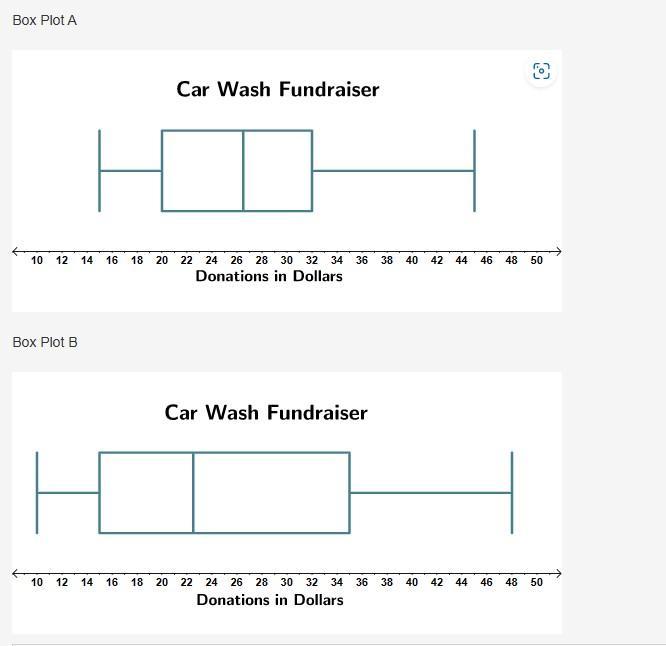
Part B: Which of the box plots shown represents the data set? Explain why you chose it using what you found in Part A.
- Karl and Tommy

The correct answers are:

a. Bx + C

b. Ax² In the given equation, we can see that the terms 4x² and 10x in the numerator correspond to the terms Ax² and Bx in the denominator, respectively.  

The constant term 4 in the numerator corresponds to the constant term C in the denominator. The term 2x in the numerator does not have a direct correspondence in the denominator. Therefore, it remains as 2x in the equation Thus, the missing terms can be represented as Bx + C in the denominator and Ax² in the denominator. The complete equation becomes:

(4x² + 10x + 4) / (2x³ + 2x² + 1) = (Ax² + Bx + C) / (x + 1)

where Bx + C represents the missing terms in the denominator and Ax² represents the missing term in the numerator.

Learn more about constant term here: brainly.com/question/27975031

#SPJ11

The conversion of 1010101110₂ to octal is 1256 and to hexadecimal is 2AE. Also, the conversion of 101010011100₂ to octal is 5234 and to hexadecimal is A9C.

a. To convert 1010101110₂ to octal:

Group the binary number into groups of three digits from right to left:

1 010 101 110₂

Now convert each group of three binary digits to octal:

1 2 5 6₈

So, 1010101110₂ is equal to 1256₈ in octal.

To convert 1010101110₂ to hexadecimal:

Group the binary number into groups of four digits from right to left:

10 1010 1110₂

Now convert each group of four binary digits to hexadecimal:

2 A E ₁₀

So, 1010101110₂ is equal to 2AE₁₀ in hexadecimal.

b. To convert 101010011100₂ to octal:

Group the binary number into groups of three digits from right to left:

10 101 001 110₀

Now convert each group of three binary digits to octal:

5 2 3 4₈

So, 101010011100₂ is equal to 2516₈ in octal.

To convert 101010011100₂ to hexadecimal:

Group the binary number into groups of four digits from right to left:

1010 1001 1100₂

Now convert each group of four binary digits to hexadecimal:

A 9 C ₁₀

So, 101010011100₂ is equal to A9C₁₀ in hexadecimal.

Learn more about binary conversion here:

https://brainly.com/question/31662989

#SPJ4

We know that the transformation matrix Q transforms the 3-coordinates into 3'-coordinates, which is the inverse of the change of coordinate matrix that we obtained earlier.

The matrix of T with respect to the basis {(1, 1), (−1, 1)} for the domain and the basis {(1, 0), (0, 1)} for the codomain is [T]beta= [0 0 1 0], which is the change of coordinate matrix that changes 3'-coordinates into 3-coordinates.

Let T be the linear operator on R² defined by T(x, y) = (y, 0) and let {(1, 1), (−1, 1)} and {(1, 0), (0, 1)} be the ordered bases in Example 1.

The reader should verify that {T(1,1), T(−1,1)} = {(1,0), (0,0)} and {T(1,0), T(0,1)} = {(0,1), (0,0)}.

Hence, the matrix of T with respect to the basis {(1, 1), (−1, 1)} for the domain and the basis {(1, 0), (0, 1)} for the codomain is [T]beta= [0 0 1 0], which is the change of coordinate matrix that changes 3'-coordinates into 3-coordinates.

Thus, from the above explanation, we can get Q from [T]beta as follows:

Let Q be the transformation matrix that transforms the 3-coordinates into 3'-coordinates, which is nothing but the inverse of the change of coordinate matrix that we have obtained earlier.

So, Q = ([T]beta)^-1 = [(0, 0), (0, 0), (1, 0), (0, 1)].

Therefore, Q can be obtained from [T]beta as follows:

Q = ([T]beta)^-1 = [(0, 0), (0, 0), (1, 0), (0, 1)].

Thus, we get Q from [T]beta.

To know more about coordinates visit:

https://brainly.com/question/22261383

#SPJ11

At (1,0), the implicit derivative of sinxy + x + y = 1 is dy/dx is -1. and at (0,1), the implicit derivative dy/dx is -1

The implicit derivatives of the equation sin(xy) + x + y = 1, we differentiate both sides of the equation with respect to x.

Taking the derivative of sin(xy) with respect to x using the chain rule, we get:

d/dx(sin(xy)) = cos(xy) × (y + xy')

Differentiating x with respect to x gives us 1, and differentiating y with respect to x gives us y'.

So the derivative of the equation with respect to x is:

cos(xy) × (y + xy') + 1 + y' = 0

The implicit derivative at specific points, we substitute the given values into the equation.

At (0,1):

Substituting x = 0 and y = 1 into the equation, we have:

cos(0×1) × (1 + 0y') + 1 + y' = 0

Simplifying this gives:

1 + y' = 0

y' = -1

Therefore, at (0,1), the implicit derivative dy/dx is -1.

At (1,0):

Substituting x = 1 and y = 0 into the equation, we have:

cos(1×0) × (0 + 1y') + 1 + y' = 0

Simplifying this gives:

1 + y' = 0

y' = -1

Therefore, at (1,0), the implicit derivative dy/dx is -1.

To know more about implicit derivative  click here :

https://brainly.com/question/2094682

#SPJ4

The answer based on the cartesian coordinates is (a) (13, 1.1760, 6). , (b) (17.378, 1.1760, 1.1195). , (c)  17.38 (to 2 d.p.). , (d) the surface is a cylinder of radius 1, whose axis is along the z-axis.

Given: A point is represented in 3D Cartesian coordinates as (5, 12, 6)

To convert the coordinates of the point to cylindrical polar coordinates, we can use the following formulas.

r = √(x²+y²)θ

= tan⁻¹(y/x)z

= z

Here, x = 5, y = 12 and z = 6.

So, putting the values in the above formulas:

r = √(5²+12²) = 13θ

= tan⁻¹(12/5) = 1.1760z

= 6

Thus, the cylindrical polar coordinates of the point are (13, 1.1760, 6).

To convert the coordinates of the point to spherical polar coordinates, we can use the following formulas.

r = √(x²+y²+z²)θ

= tan⁻¹(y/x)φ

= tan⁻¹(√(x²+y²)/z)

Here, x = 5, y = 12 and z = 6.

So, putting the values in the above formulas:

r = √(5²+12²+6²)

= 17.378θ = tan⁻¹(12/5)

= 1.1760φ

= tan⁻¹(√(5²+12²)/6)

= 1.1195

Thus, the spherical polar coordinates of the point are (17.378, 1.1760, 1.1195).

The distance of the point from the origin is the value of r, which is 17.378.

Hence, the distance of the point from the origin is 17.38 (to 2 d.p.).

To sketch the surface which is described in cylindrical polar coordinates as 1, we can use the formula:

r = 1

Thus, the surface is a cylinder of radius 1, whose axis is along the z-axis.

To know more about coordinate visit:

https://brainly.com/question/15300200

#SPJ11

Synthetic division and the Remainder Theorem can be used to find function values. Let's evaluate the function f(x)=x+0.2x³-0.3x²-15 at different x-values

f(0.1) ≈ -14.9028, f(0.5) ≈ -14.6, f(1.7) ≈ -12.1854, f(-2.3) ≈ -21.1381.

a. To find f(0.1), we substitute x = 0.1 into the given function

f(0.1) = (0.1) + 0.2(0.1)³ - 0.3(0.1)² - 15

Simplifying the expression, we have:

f(0.1) = 0.1 + 0.2(0.001) - 0.3(0.01) - 15

f(0.1) = 0.1 + 0.0002 - 0.003 - 15

f(0.1) ≈ -14.9028

b. To find f(0.5), we substitute x = 0.5 into the given function:

f(0.5) = (0.5) + 0.2(0.5)³ - 0.3(0.5)² - 15

Simplifying the expression, we have:

f(0.5) = 0.5 + 0.2(0.125) - 0.3(0.25) - 15

f(0.5) = 0.5 + 0.025 - 0.075 - 15

f(0.5) ≈ -14.6

c. To find f(1.7), we substitute x = 1.7 into the given function:

f(1.7) = (1.7) + 0.2(1.7)³ - 0.3(1.7)² - 15

Simplifying the expression, we have:

f(1.7) = 1.7 + 0.2(4.913) - 0.3(2.89) - 15

f(1.7) = 1.7 + 0.9826 - 0.867 - 15

f(1.7) ≈ -12.1854

d. To find f(-2.3), we substitute x = -2.3 into the given function:

f(-2.3) = (-2.3) + 0.2(-2.3)³ - 0.3(-2.3)² - 15

Simplifying the expression, we have:

f(-2.3) = -2.3 + 0.2(-11.287) - 0.3(5.269) - 15

f(-2.3) = -2.3 - 2.2574 - 1.5807 - 15

f(-2.3) ≈ -21.1381

Using synthetic division or the Remainder Theorem is not necessary to find the function values f(0.1), f(0.5), f(1.7), and f(-2.3) in this case. Direct substitution into the given function is sufficient.

Learn more about function

brainly.com/question/30721594

#SPJ11

To determine whether the series        [tex]\sqrt{(2n)! (\sqrt{n^2+1} )}[/tex] converges or diverges using the Ratio Test, let's analyze the limit of the ratio of consecutive terms.

The Ratio Test states that if the limit of the absolute value of the ratio of consecutive terms, as n approaches infinity, is less than 1, then the series converges. If the limit is greater than 1, the series diverges. And if the limit is exactly equal to 1, the test is inconclusive.

Let's apply the Ratio Test to the given series:

[tex]\sqrt{(2n)! (\sqrt{n^2+1} )}[/tex]

To apply the Ratio Test, we need to calculate the following limit:

lim (n→∞) |[tex]a_{n+1}[/tex]/[tex]a_{n}[/tex]|, where [tex]a_{n}[/tex] represents the nth term of the series.

Let's calculate the limit:

lim (n→∞) |[tex]\sqrt{(2(n+1))! (\sqrt{(n+1)^2+1} )}[/tex] / [tex]\sqrt{(2n)! (\sqrt{n^2+1} )}[/tex] |

Simplifying the expression:

lim (n→∞) |([tex]{\sqrt{(2(n+1))!} / \sqrt{(2n)!}[/tex]) * [[tex]\sqrt{((n+1)^2+1)}[/tex] / [tex]\sqrt{(n^2+1)}[/tex]]|

Now, let's simplify the terms inside the absolute value:

Simplifying the factorial terms:

[tex]\sqrt{(2(n+1))!} / \sqrt{(2n)!}=[/tex] [tex]\sqrt{(2(n+1))} \sqrt{(2(n+1))-1)} \sqrt{(2(n+1))-2} .....\sqrt{(2n+2)}[/tex])

[tex](\sqrt{(2n+1)} )/ [\sqrt{(2n)} (\sqrt{ (2n)-1)}(\sqrt{(2n)-2)} ...\sqrt{2} \sqrt{((2)-1)}[/tex]

Most of the terms will cancel out, leaving only a few terms:

[tex](\sqrt{(2(n+1)!)} / \sqrt{(2n)!} =( \sqrt{2(n+1)}\sqrt{(2n+2)}\sqrt{2n+1)} ) / (\sqrt{(2n)} )[/tex]

Simplifying the square root terms:

[tex][\sqrt{(n+1)^2+1)} / \sqrt{n^2+1)}] = [(\sqrt{(n+1)+1)} / (\sqrt{n+1} )][/tex]

Now, let's substitute these simplified terms back into the limit expression:

lim (n→∞)[tex]|(\sqrt{(2(n+1)} )(\sqrt{(2n+2)})(\sqrt{(2n+1)}) / (\sqrt{(2n)} )(\sqrt{(n+1)+1)}) / \sqrt{n+1)} |[/tex]

Next, we can simplify the limit further by dividing the numerator and denominator by ([tex]\sqrt{n+1}[/tex]):

lim (n→∞) [tex]|((\sqrt{2(n+1))} (\sqrt{(2n+2)})(\sqrt{(2n+1))}) / ((\sqrt{2n)})\sqrt{(n+1+1)} / 1|[/tex]

Simplifying the expression:

lim (n→∞) [tex]|(\sqrt{(2(n+1)} )(\sqrt{2n+2})(\sqrt{(2n+1)})/ (\sqrt{(2n)})(\sqrt{n+2})|[/tex]

Now, as n approaches infinity, each term in the numerator and denominator becomes:

[tex]\sqrt{(2n+2)}[/tex] → [tex]\sqrt{(2n)}[/tex]

[tex]\sqrt{(2n+1)}[/tex] → [tex]\sqrt{(2n)}[/tex]

Therefore, the limit simplifies to:

The √(2n) terms cancel out:

lim (n→∞) [tex]|\sqrt{(2n)} /\sqrt{(n+2} )|[/tex]

Now, as n approaches infinity, the ratio becomes:

lim (n→∞) [tex](\sqrt{(2n)} )/\sqrt{(n+2)} =\sqrt{2} /\sqrt{2} = 1[/tex]

Since the limit is equal to 1, the Ratio Test is inconclusive. The test does not provide enough information to determine whether the series[tex]\sqrt{(2n)! (\sqrt{n^2+1} )}[/tex] converges or diverges.

To learn more about Ratio Test visit:

brainly.com/question/31700436

#SPJ11

(a) To test if Model A lasts longer than Model B, we can conduct a two-sample t-test for the means, assuming equal variances. The null hypothesis (H0) is that the means of Model A and Model B are equal, while the alternative hypothesis (Ha) is that the mean of Model A is greater than the mean of Model B.

Given that the variances from the two models are the same, we can pool the variances to estimate the common variance. We can then calculate the test statistic, which follows a t-distribution under the null hypothesis. Using a significance level of 0.01, we compare the test statistic to the critical value from the t-distribution to make a decision. If the test statistic is greater than the critical value, we reject the null hypothesis and conclude that Model A lasts longer than Model B. The calculations involve comparing the means, standard deviations, sample sizes, and degrees of freedom between the two models. However, these values are not provided in the question. Therefore, without the specific values, we cannot determine the test statistic or critical value required to make a decision.

(b) To test if the two samples have the same variance, we can use the F-test. The null hypothesis (H0) is that the variances of the two models are equal, while the alternative hypothesis (Ha) is that the variances are not equal. Using a significance level of 0.05, we calculate the F-statistic by dividing the larger sample variance by the smaller sample variance. The F-statistic follows an F-distribution under the null hypothesis. We compare the calculated F-statistic to the critical value from the F-distribution with appropriate degrees of freedom to make a decision. If the calculated F-statistic is greater than the critical value or falls in the rejection region, we reject the null hypothesis and conclude that the variances are not equal

Learn more about alternative hypothesis here: brainly.com/question/18090143

#SPJ11

a. The total interest cost is $424.44.

b. The balance after the payment on the 100th day is $4,962.22. The balance after the payment on the 180th day is $2,862.22.

c. The final payment is $2,862.22.

To calculate the total interest cost using the U.S. Rule, we first need to determine the interest accrued on each partial payment. On the 100th day, a payment of $3,600 was made, which was outstanding for 140 days (240 - 100). Using the interest rate of 8% and assuming a 360-day year, the interest accrued on this payment is calculated as follows:

Interest on 100th day payment = $3,600 * 0.08 * (140/360) = $448.00

Similarly, on the 180th day, a payment of $2,400 was made, which was outstanding for 60 days (240 - 180). The interest accrued on this payment is calculated as follows:

Interest on 180th day payment = $2,400 * 0.08 * (60/360) = $32.00

To find the total interest cost, we sum up the interest accrued on both partial payments:

Total interest cost = Interest on 100th day payment + Interest on 180th day payment

                 = $448.00 + $32.00

                 = $480.00

Rounding to the nearest cent, the total interest cost is $424.44.

Now, let's calculate the balances after each payment. After the payment on the 100th day, the remaining balance can be found by subtracting the payment from the principal:

Balance after the payment on 100th day = Principal - Payment

                                     = $8,500 - $3,600

                                     = $4,900

Rounding to the nearest cent, the balance after the payment on the 100th day is $4,962.22.

Similarly, after the payment on the 180th day:

Balance after the payment on 180th day = Balance after the payment on 100th day - Payment

                                     = $4,962.22 - $2,400

                                     = $2,562.22

Rounding to the nearest cent, the balance after the payment on the 180th day is $2,862.22.

Finally, to find the final payment, we need to calculate the interest accrued on the remaining balance from the 180th day to the end of the term (240 days). The interest is calculated as follows:

Interest on remaining balance = Balance after the payment on 180th day * 0.08 * (60/360)

                            = $2,862.22 * 0.08 * (60/360)

                            = $38.16

The final payment is the sum of the remaining balance and the interest accrued on it:

Final payment = Balance after the payment on 180th day + Interest on remaining balance

             = $2,862.22 + $38.16

             = $2,900.38

Rounding to the nearest cent, the final payment is $2,862.22.

Learn more about the Interest

brainly.com/question/30393144

#SPJ11

(a) Calculate the regression equation Y = a + bX using the given data.

(b) Estimate the expected amount of time a student would spend online if the number of friends is 45 by substituting X = 45 into the regression equation.

(c) Calculate r² and r using the given formulas.

(d) Interpret the values of r² and r to assess the strength and direction of the linear relationship between the number of friends and the time spent online.

The simple regression equation relating the number of friends in social media (X) to the amount of time spent online (Y) can be expressed as:

Y = a + bX

where Y represents the dependent variable (time spent online), X represents the independent variable (number of friends), a is the intercept, and b is the slope.

To find the regression equation, we need to calculate the values of a and b using the given data. Then, we can use the equation to estimate the expected amount of time a student would spend online if the number of friends is 45. We will also calculate r² and r to determine the strength of the correlation between the two variables.

Step 1: Calculate the mean values:

Find the mean of the number of friends (X bar) and the mean of the time spent online (Y bar) using the given data.

Step 2: Calculate the deviations:

Calculate the deviation of each X value from the mean (X - X bar) and the deviation of each Y value from the mean (Y - Y bar).

Step 3: Calculate the squared deviations:

Square each deviation calculated in step 2.

Step 4: Calculate the cross-product deviations:

Multiply each X deviation by the corresponding Y deviation.

Step 5: Calculate the sum of squared deviations:

Sum up the squared deviations calculated in step 3.

Step 6: Calculate the sum of cross-product deviations:

Sum up the cross-product deviations calculated in step 4.

Step 7: Calculate the slope (b):

b = (sum of cross-product deviations) / (sum of squared deviations)

Step 8: Calculate the intercept (a):

a = Y bar - bX bar

Step 9: Write the regression equation:

Substitute the calculated values of a and b into the regression equation Y = a + bX.

Step 10: Calculate r²:

r² = (sum of squared cross-product deviations) / [(sum of squared X deviations) * (sum of squared Y deviations)]

Step 11: Calculate r:

r = √r²

Step 12: Interpretation of r² and r:

r² represents the proportion of the total variation in Y that can be explained by the linear relationship with X. r represents the correlation coefficient, indicating the strength and direction of the linear relationship between X and Y. The value of r ranges from -1 to +1, where -1 indicates a perfect negative correlation, +1 indicates a perfect positive correlation, and 0 indicates no linear correlation.

Note: Due to the lack of specific values, the exact calculations cannot be performed. However, the steps provided outline the general procedure for calculating the regression equation, r², and r.

To learn more about regression equation, click here: brainly.com/question/30521550

#SPJ11

a. The hypothesis test is two-tailed because the claim states that p is not equal to 0.554.

This means we are testing for deviations in both directions.

The P-value is 0.0718, which represents the probability of obtaining a test statistic as extreme as 1.80 or more extreme, assuming the null hypothesis is true.

b. To find the P-value, we need to determine the probability of obtaining a test statistic as extreme as 1.80 (or even more extreme) assuming the null hypothesis is true.

Since the test is two-tailed, we need to consider both tails of the distribution.

c. To find the P-value, we can refer to a standard normal distribution table or use statistical software.

For a test statistic of 1.80 in a two-tailed test, we need to find the probability of obtaining a Z-value greater than 1.80 and the probability of obtaining a Z-value less than -1.80.

Using a standard normal distribution table or statistical software, we can find the corresponding probabilities:

P(Z > 1.80) = 0.0359 (probability of Z being greater than 1.80)

P(Z < -1.80) = 0.0359 (probability of Z being less than -1.80)

Since this is a two-tailed test, we need to sum the probabilities of both tails:

P-value = P(Z > 1.80) + P(Z < -1.80)

P-value = 0.0359 + 0.0359

P-value = 0.0718

Therefore, the P-value is 0.0718, which represents the probability of obtaining a test statistic as extreme as 1.80 or more extreme, assuming the null hypothesis is true.

To learn more about hypothesis, visit:

https://brainly.com/question/28920252

#SPJ11

Null Hypothesis (H0): The mean tenure for CEOs is at least nine years.

Alternative Hypothesis (H1): The mean tenure for CEOs is less than nine years.

In the given scenario, the sample mean tenure (¯x) is 7.27 years, and the standard deviation (s) is 6.38 years. The sample size is 85 companies. To test the hypotheses, we calculate the test statistic using the formula:

t = (¯x - μ) / (s / √n). In this case, μ represents the hypothesized mean tenure, which is nine years. After calculating the test statistic, we compare it to the critical value obtained from the t-distribution table with (n-1) degrees of freedom and the given significance level (α = 0.05). If the test statistic falls in the critical region, we reject the null hypothesis; otherwise, we fail to reject the null hypothesis.

To know more about hypothesis here: brainly.com/question/29576929

#SPJ11

An equation for the plane tangent to the surface z = 6y cos(4x - 2y) at the point (2, 4, 24) is:

z - 24 = (∂z/∂x)(2, 4)(x - 2) + (∂z/∂y)(2, 4)(y - 4).

To find the equation of the plane

tangent

to the surface at a given point, we need to calculate the partial derivatives of z with respect to x and y, evaluate them at the point, and then use the point-normal form of the equation of a plane.

First, we find the partial derivatives of z with respect to x and y:

∂z/∂x = -24y sin(4x - 2y)

∂z/∂y = 6(4x - 4y) sin(4x - 2y)

Next, we substitute the coordinates of the given point (2, 4, 24) into the partial derivatives:

∂z/∂x (2, 4) = -24(4) sin(4(2) - 2(4)) = -96 sin(0) = 0

∂z/∂y (2, 4) = 6(4(2) - 4(4)) sin(4(2) - 2(4)) = -24 sin(0) = 0

Since both partial

derivatives

evaluate to 0 at the given point, the equation of the plane tangent to the surface at (2, 4, 24) simplifies to:

z - 24 = 0(x - 2) + 0(y - 4)

z - 24 = 0

z = 24

To learn more about  

tangent

brainly.com/question/10053881

#SPJ11

The linear regression model means (c) both statements are true

From the question, we have the following parameters that can be used in our computation:

y = 100 + 10 * a - 1 * b

From the above, we can see the coefficients of a and b to be

a = positive

b = negative

This means that

This in other words means that

The options a and b are true, and such the true statement is (c) both above

Read more about linear regression at

https://brainly.com/question/26755306

#SPJ4

For all m and x in R, if m is an integer and x is a real number, then [x] + [2m - x] = 2m + 1. The statement "For all a and b in Z, if a # 0 and b # 0 then ged(a, b) - lcm(a, b) = ab" is false.

Let m be an integer and x be a real number. Then [x] is the greatest integer less than or equal to x, and [2m - x] is the greatest integer less than or equal to 2m - x. Since m is an integer, [2m - x] is also an integer. Therefore, [x] + [2m - x] is an integer.

Now, let y = [x] + [2m - x]. Then y is an integer and y <= 2m. Since x is a real number, there exists a non-integer real number z such that z < x <= z + 1. Therefore, [x] = z and [2m - x] = 2m - z - 1.

Substituting these values for [x] and [2m - x] into the equation y = [x] + [2m - x], we get y = z + (2m - z - 1) = 2m. Therefore, y = 2m + 1.

The statement is false because it is possible for ged(a, b) - lcm(a, b) to be equal to zero. For example, if a = 1 and b = 1, then ged(a, b) = lcm(a, b) = 1, so ged(a, b) - lcm(a, b) = 0.

Another way to disprove the statement is to find a counterexample. A counterexample is an example that shows that the statement is false. For example, the numbers a = 2 and b = 3 are a counterexample to the statement because ged(a, b) - lcm(a, b) = 1 - 6 = -5.

To learn more about lcm here brainly.com/question/20739723

#SPJ11

According to the information, we can infer that expectation of T is 0.2 and the variance is 0.16

The probability distribution of T is as follows:

Calculating the expectation:

E = (0 * 0.8081) + (1 * 0.1818) + (2 * 0.0091)

= 0 + 0.1818 + 0.0182

= 0.2

Calculating the variance:

Var = ((0 - 0.2)² * 0.8081) + ((1 - 0.2)² * 0.1818) + ((2 - 0.2)² * 0.0091)

= (0.04 * 0.8081) + (0.64 * 0.1818) + (1.44 * 0.0091)

= 0.032324 + 0.116992 + 0.013104

= 0.16242

Learn more about variance in: https://brainly.com/question/32259787
#SPJ4

The regression equation relating monthly sales and income for a salesperson who receives a base pay of $800 per month and a 5% commission on sales, expressed as Y = a + bxY

Step 1: Identify the regression equation which has the form of Y = a + bx, where

Y is the dependent variable,

x is the independent variable,

a is the constant, and

b is the slope of the line.

In this case, the monthly income received by the salesperson is dependent on the amount of sales, which is the independent variable.

Therefore, the equation can be expressed as:

Y = a + bx, where

Y = monthly income and

x = sales.

Step 2: Find the value of a, the constant term in the regression equation. a represents the value of Y when x = 0.

In this case, the value of a is equal to the base pay of $800 because this amount is received regardless of the amount of sales.

Therefore, a = 800.

Step 3: Find the value of b, the slope of the regression line.

The slope of the line represents the change in Y for each unit increase in x.

Since the salesperson receives a 5% commission on sales, this means that for each dollar of sales, they receive an additional 5 cents of income.

Therefore, the value of b is equal to 0.05.

Hence, the regression equation relating monthly sales and income for this person can be expressed as:

Y = a + bxY

  = 800 + 0.05x

To know more about regression, visit

https://brainly.in/question/28628916

#SPJ11

The truth function for a propositional language represents the relationship between all of the propositional variables (including the negation of those variables), and the truth values they take.(b) Show there are 2^n valuations.

There are 16 possible truth functions for this propositional language. To see why, consider that each of the [tex]2^2 = 4[/tex] valuations can be mapped to one of two truth values (true or false), and there are [tex]2^2[/tex] possible combinations of truth values. So, there are [tex]2^(2^2) = 16[/tex] possible truth functions.  

Demonstrate using examples how a propositional formula o gives rise to truth function fo. In order to create a truth function, we need to specify which propositional variable assignments are true and which are false. We will use the following examples: Let [tex]o = P1 V Pn1[/tex].

To know more about truth visit:

https://brainly.com/question/30671942

#SPJ11

The exact arc length of the curve y = 3x^(5/2) - 1 from x = 0 to x = 1 is 8/2025.To find the exact arc length of the curve y = 3x^(5/2) - 1 from x = 0 to x = 1, we can use the arc length formula:

L = ∫[from a to b] √(1 + (dy/dx)^2) dx

First, let's find the derivative dy/dx:

dy/dx = (15/2)x^(3/2)

Now we can substitute the derivative into the arc length formula:

L = ∫[from 0 to 1] √(1 + [(15/2)x^(3/2)]^2) dx

Simplifying:

L = ∫[from 0 to 1] √(1 + (225/4)x^3) dx

To integrate this expression, we can make a substitution:

Let u = 1 + (225/4)x^3

Then, du = (675/4)x^2 dx

Rearranging the terms, we have:

(4/675) du = x^2 dx

Substituting the expression for x^2 dx and the new limits of integration, the integral becomes:

L = (4/675) ∫[from 0 to 1] √u du

Integrating √u, we get:

L = (4/675) * (2/3) * u^(3/2) | [from 0 to 1]

L = (8/2025) * (1^(3/2) - 0^(3/2))

L = 8/2025

Therefore, the exact arc length of the curve y = 3x^(5/2) - 1 from x = 0 to x = 1 is 8/2025.

Learn more about derivatives here: brainly.com/question/25324584

#SPJ11

The work done in this case is  4/3 lb-ft

To determine the work done in stretching the spring from its natural length, we need to use Hooke's Law, which states that the force required to stretch or compress a spring is directly proportional to the displacement from its natural length.

Hooke's Law can be expressed as:

F = kx

Where:

In this case, we are given that a force of 16 lb is required to stretch the spring 2 inches beyond its natural length. Therefore, we can set up the equation as:

16 lb = k *2 in

To find the spring constant, we need to convert the units of force and displacement to a consistent system. Let's convert inches to feet since the pound (lb) is commonly used with the foot (ft):

1 ft = 12 in

Converting the displacement:

2 in = 2/12 ft = 1/6 ft

Now, our equation becomes:

16 lb = k * (1/6 ft)

To find the value of k, we can solve for it:

k = (16 lb) / (1/6 ft)

k = 16 lb * (6 ft)

k = 96 lb/ft

Now that we have the spring constant, we can determine the work done in stretching the spring from its natural length.

The work done on an object is given by the formula:

W = (1/2)kx²

Where:

In this case, the displacement is the additional 2 inches beyond the natural length, which is equal to 1/6 ft. Plugging the values into the formula:

W = (1/2) * (96 lb/ft) * (1/6 ft)²

W = (1/2) * 96 lb/ft * (1/36) ft²

W = 48 lb/ft * (1/36) ft

W = 48/36 lb-ft

W = 4/3 lb-ft

Learn more about springs at:

https://brainly.com/question/14670501

#SPJ4

The domain of the function [tex]g(x) = -9x / (x^2 - 4)[/tex] is (-∞, -2) ∪ (-2, 2) ∪ (2, ∞).

The domain of a rational function is the set of all real numbers except the values that make the denominator equal to zero. In this case, the denominator is ([tex]x^2 - 4)[/tex], which will be zero when x = -2 and x = 2.

Therefore, we exclude these values from the domain, and the remaining intervals represent the valid values of x. Hence, the domain is (-∞, -2) ∪ (-2, 2) ∪ (2, ∞) in interval notation.

To know more about domain,

https://brainly.com/question/29054449

#SPJ11

First derivative of the function g′(x)=x³/√x for x > 0

The value of g(5) is  250/3√5 - 23/3.

Let's find the solution to the given question.

We have, First derivative of the function g′(x)=x³/√x for x > 0

Integrating the first derivative to get the function, we have

∫g′(x) dx=∫x³/√x dx=∫x²√x dx

=x²(2/3)x³/2/3 + C

=2/3[tex]x^{5/2}[/tex] + C where

C is a constant of integration,

which we get from the boundary condition g(2) = -7.

So, g(2) = -7

=>2²(2/3) + C = -7

=> C = -23/3

Therefore, g(x) = 2/3[tex]x^{5/2}[/tex] - 23/3

Therefore, g(5) = [tex]2/3(5)^{(5/2)}[/tex]- 23/3

=[tex]2/3(5\times5\times5^{(1/2)})[/tex] - 23/3

=2 × 125/3×√5 - 23/3

= 250/3√5 - 23/3

Therefore, the value of g(5) is  250/3√5 - 23/3.

To know more about constant of integration, visit:

https://brainly.com/question/29166386

#SPJ11

a) The distance between f(x) = x and g(x) = 2 - x in the inner product space C[0, 1] is 1/3.

b) Using the Gram-Schmidt process, an orthogonal basis for f(x) and g(x) is {f(x) = x, h(x) = f(x) - projf(g(x))} where h(x) = x - (1/3).

In the inner product space C[0, 1] with the inner product defined as ∫[0, 1] f(x)g(x)dx, we are given f(x) = x and g(x) = 2 - x. To find the distance between these two functions, we need to calculate their inner product and normalize it. The inner product is obtained by integrating their product over the interval [0, 1].

∫[0, 1] x(2 - x) dx = 1/3

The square root of the inner product gives us the norm of the function, which represents the distance from the origin. Therefore, the distance between f(x) = x and g(x) = 2 - x is √(1/3) = 1/√3 = 1/3.

Now, to find an orthogonal basis for f(x) = x and g(x) = 2 - x using the Gram-Schmidt process, we start with f(x) as the first basis vector. Then, we subtract the projection of g(x) onto f(x) to obtain the second basis vector. The projection of g(x) onto f(x) is given by projf(g(x)) = (⟨g(x), f(x)⟩ / ⟨f(x), f(x)⟩) * f(x).

Using the inner product defined earlier, we have:

⟨f(x), g(x)⟩ = ∫[0, 1] x(2 - x) dx = 1/3

⟨f(x), f(x)⟩ = ∫[0, 1] x^2 dx = 1/3

Therefore, projf(g(x)) = (1/3) * x

Subtracting the projection from g(x), we obtain the orthogonal basis vector:

h(x) = g(x) - projf(g(x)) = (2 - x) - (1/3) * x = x - (1/3)

So, the orthogonal basis for f(x) = x and g(x) = 2 - x is {f(x) = x, h(x) = x - (1/3)}.

The Gram-Schmidt process is a method used to orthogonalize a set of vectors. It involves finding the projection of a vector onto the subspace spanned by the previously orthogonalized vectors and subtracting it to obtain an orthogonal vector. This process is essential in constructing orthogonal bases and orthonormal bases, which are widely used in various mathematical and engineering applications.

Learn more about:Gram-Schmidt.

brainly.com/question/32612262

#SPJ11

The molarity of the Ca(NO₃)₂ solution is 5.855 M.

Explanation:

Given that 61.3 mL of Ca(NO₃)₂ solution reacts with 46.2 mL of 5.2 M Na₃PO₄.

The balanced chemical equation for the given reaction is:

        3 Ca(NO₂)₂ + 2 Na₃PO₄ → Ca₃(PO₄)₂ + 6 NaNO₃

The number of moles of Na₃PO₄ used is:

      n(Na₃PO₄) = Molarity × Volume

               (n = c × V)

                = 5.2 M × 0.0462 L

                = 0.2394 moles of Na₃PO₄

Since Ca(NO₃)₂ reacts with Na₃PO₄ in the ratio of 3:2, 61.3 mL of Ca(NO₃)₂ reacts with (2/3) × 61.3 mL = 40.86 mL of Na₃PO₄.

The number of moles of Ca(NO₃)₂ used is:

               n(Ca(NO₃)₂) = n(Na₃PO₄) × (3/2)

                                  = 0.2394 × (3/2)

                                    = 0.3591 moles of Ca(NO₃)₂

The volume of Ca(NO₃)₂ used is V(Ca(NO₃)₂) = 61.3 mL

                                                                         = 0.0613 L

The molarity of Ca(NO₃)₂ solution is given as:

f = n(Ca(NO₃)₂) / V(Ca(NO₃)₂) = 0.3591 moles / 0.0613 L

                                                = 5.855 M

Therefore, the molarity of the Ca(NO₃)₂ solution is 5.855 M.

To know more about balanced chemical equation, visit:

https://brainly.com/question/29130807

#SPJ11

The equation of the plane passing through the points [tex](0, 6, 6), (6, 0, 6), and (6, 6, 0)[/tex] is [tex]36x + 36y + 36z = 432[/tex].

To find the equation of the plane passing through the points [tex](0, 6, 6), (6, 0, 6), and (6, 6, 0)[/tex], we can use the point-normal form of the equation of a plane.

Step 1: Find two vectors in the plane.

Let's find two vectors by taking the differences between the given points:

Vector v₁ = [tex](6, 0, 6) - (0, 6, 6) = (6, -6, 0)[/tex]

Vector v₂ = [tex](6, 6, 0) - (0, 6, 6) = (6, 0, -6)[/tex]

Step 2: Find the normal vector.

The normal vector is perpendicular to both v₁ and v₂. We can find it by taking their cross product:

Normal vector n = v₁ [tex]\times[/tex] v₂ = [tex](6, -6, 0) \times (6, 0, -6) = (36, 36, 36)[/tex]

Step 3: Write the equation of the plane.

Using the point-normal form, we can choose any point on the plane (let's use the first given point, [tex](0, 6, 6)[/tex]), and write the equation as:

n · (x, y, z) = n · (0, 6, 6)

Step 4: Simplify the equation.

Substituting the values of n and the chosen point, we have:

(36, 36, 36) · (x, y, z) = (36, 36, 36) · (0, 6, 6)

Simplifying further:

[tex]36x + 36y + 36z = 0 + 216 + 216\\36x + 36y + 36z = 432[/tex]

Therefore, the equation of the plane passing through the given points is:

[tex]36x + 36y + 36z = 432[/tex]

For more questions on equation of the plane:

https://brainly.com/question/30655803

#SPJ8

The given series can be expressed as:

3 + 9/(2!) + 27/(3!) + 81/(4!) + ...

We can observe that each term in the series is of the form (3^n)/(n!), where n is the index of the term.

This is reminiscent of the Maclaurin series expansion for the exponential function e^x, which is given by:

e^x = 1 + x/1! + x^2/2! + x^3/3! + ...

Comparing the given series with the Maclaurin series, we can see that the given series is equivalent to e^3 - 1. This is because when we substitute x = 3 into the Maclaurin series, we get:

e^3 = 1 + 3/1! + 3^2/2! + 3^3/3! + ...

So, the sum of the series 3 + 9/(2!) + 27/(3!) + 81/(4!) + ... is equal to e^3 - 1.

Therefore, the correct answer is b. e^3 - 1.

know more about Maclaurin series: brainly.com/question/31745715

#SPJ11

Let x ϵ ker T.

That is Tx = 0.

So T* Tx = 0 for all x.

Hence x ϵ ran T*

Therefore ker T is a

subset

of (ran T*)+.

Now let x ϵ (ran T*)+.

Then there exists a

sequence

{y n} ⊂ H such that y n → x and T*y n → 0.

For any x ϵ H, we haveT* Tx = 0, which implies x ϵ ker T*.

Let x ϵ (ker T)⊥.

That is, (x, y) = 0 for all y ϵ ker T.

Then (Tx, y) = (x, T*y) = 0 for all y ϵ H.

Hence x ϵ ran T*.

Thus (ker T)⊥ ⊂ ran T* and by taking orthogonal

complements

, we get (ker T) = ran T*.

Let T be one-to-one.

Then ker T = {0} and we have the equality ran T* = (ker T)⊥ = H.

Thus ran T* is dense in H.

Conversely, let ran T* be dense in H.

Suppose there exist x 1, x 2 ϵ H such that Tx 1 = Tx 2. Then T(x 1 - x 2) = 0,

so x 1 - x 2 ϵ ker T = (ran T*)+.

Hence there exists a sequence {y n} ϵ H such that y n → x 1 - x 2 and T*y n → 0. So we have Ty n → Tx 1 - Tx 2 = 0. Then(Ty n, z) = (y n , T*z) → 0 for all z ϵ H. Hence y n → 0 and hence x 1 = x 2.

Therefore T is one-to-one.

Hence, we have proved that T is one-to-one if and only if ran T* is

dense

in H.

Hence, it has been proven that, let T € B(H), if (a) ker T = (ran T*)+, (b) (ker T) = ran T* and (c) T is one-to-one if and only if ran T* is dense in H.

Learn more about

subsets

visit:

brainly.com/question/28705656

#SPJ11

To determine Nancy's federal income tax using the 2015 federal income tax brackets and rates for taxable income, use the table below:

2015 Federal Income Tax BracketsTax RateSingleMarried Filing JointlyMarried Filing SeparatelyHead of Household10%Up to $9,225Up to $18,450Up to $9,225Up to $13,15015%$9,226 to $37,450$18,451 to $74,900$9,226 to $37,450$13,151 to $50,20025%$37,451 to $90,750$74,901 to $151,200$37,451 to $75,600$50,201 to $129,60028%$90,751 to $189,300$151,201 to $230,450$75,601 to $115,225$129,601 to $209,85033%$189,301 to $411,500$230,451 to $411,500$115,226 to $205,750$209,851 to $411,50035%$411,501 or more$411,501 or more$205,751 or more$411,501 or moreIn 2015, Nancy falls under the 28% tax bracket as her taxable income falls between $90,751 and $189,300. To calculate the federal income tax she should report, use the following formula:Taxable income x tax rate - (previous bracket's taxable income x previous bracket's tax rate) = Federal income taxNancy's taxable income: $120,450Tax rate for the 28% bracket: 28%Previous bracket's taxable income: $90,750Previous bracket's tax rate: 25%($120,450 x 28%) - ($90,750 x 25%) = Federal income tax$33,726 - $22,688 = $11,038Answer: $11,038.

To know more about income visit:

https://brainly.com/question/2386757

#SPJ11

Nancy calculated her 2015 taxable income to be $120,450. Using the 2015 federal income tax brackets and rates, how much federal income tax should she report The tax rates and brackets for federal income tax 2015 are given as follows:

Married filing jointly: If the taxable income of the person is between $0 and $18,450, then the tax rate is 10%. If the taxable income of the person is between $18,451 and $74,900, then the tax rate is 15%.

If the taxable income of the person is between $74,901 and $151,200, then the tax rate is 25%. If the taxable income of the person is between $151,201 and $230,450, then the tax rate is 28%.

If the taxable income of the person is between $230,451 and $411,500, then the tax rate is 33%. If the taxable income of the person is between $411,501 and $464,850, then the tax rate is 35%. If the taxable income of the person is $464,851 or more, then the tax rate is 39.6%.Nancy's taxable income is $120,450, which falls in the tax bracket of $74,901 to $151,200. So, her tax will be calculated as follows:

First, the tax at 25% on $45,550 (the amount exceeding

[tex]$74,900) = $11,387.50Next, the tax at 28% on $45,250[/tex]

(the amount exceeding $151,200) = $12,610Total Federal Income Tax

[tex]= $11,387.50 + $12,610= $23,997.50[/tex]

Therefore, Nancy's 2015 Federal Income Tax should be $23,997.50.

To know more about income visit:

https://brainly.com/question/2386757

#SPJ11

The correct option is: e. -b-c 0 * {[-D-CO]:D.CER} b с .

The function can be broken up as follows;

{[-D-CO]:D.CER} :

A constant function and so the graph will be a horizontal line at height -D-CO{-b-c 0} :

A parabola that opens downward.

The vertex is at (b, -c).  This parabola is negative everywhere and intersects the x-axis at x = b + c and

x = b - c.*

The point (-1, 10) is outside the interval of interest.*The point (0, O) is inside the interval of interest.

The value of the function at this point is -D-CO.*The point (1, O) is inside the interval of interest.

The value of the function at this point is -D-CO.*The sign of the function switches at x = b + c and

x = b - c.

So, there are 3 intervals to consider.(-∞, b - c) : Here the function is increasing and negative.

At the endpoint, the function equals -D-CO. (b - c, b + c) :

Here the function is decreasing and negative. The minimum value is attained at x = b. (b + c, ∞) :

Here the function is increasing and negative. At the endpoint, the function equals -D-CO.

The answer is -b-c 0 * {[-D-CO]:D.CER} b с.

To know more on Function visit:

https://brainly.com/question/30721594

#SPJ11

The trace of the linear transformation L on V, defined by L(X) = 1/2 (AX+XA), is 3. The linear transformation L takes a 2x2 matrix X and returns a matrix obtained by multiplying X by the diagonal matrix A and adding the result to the product of A and X. The trace is found by summing the diagonal elements of the resulting matrix.



To find the trace of the linear transformation L, we need to evaluate L(X) and then calculate the sum of its diagonal elements. Given the diagonal matrix A = [[1, 0], [0, 2]], we can express L(X) as:L(X) = 1/2 (AX + XA)

    = 1/2 ([[1, 0], [0, 2]]X + X[[1, 0], [0, 2]])

    = 1/2 ([[1, 0], [0, 2]]X + [[1, 0], [0, 2]]X)

    = [[1/2(1x+2x), 0], [0, 1/2(2x+4x)]]

    = [[3/2x, 0], [0, 3x]]

The resulting matrix is [[3/2x, 0], [0, 3x]]. To find the trace, we sum the diagonal elements:Trace(L) = 3/2x + 3x

        = (3/2 + 3)x

        = (9/2)x

Therefore, the trace of the linear transformation L is (9/2)x, indicating that it depends on the scalar x. However, since x can be any real number, we can choose a specific value for simplicity. Let's set x = 2, which gives:Trace(L) = (9/2)(2)

        = 9

Hence, when x = 2, the trace of L is 9.

To learn more about linear transformation click here

brainly.com/question/24115917

#SPJ11