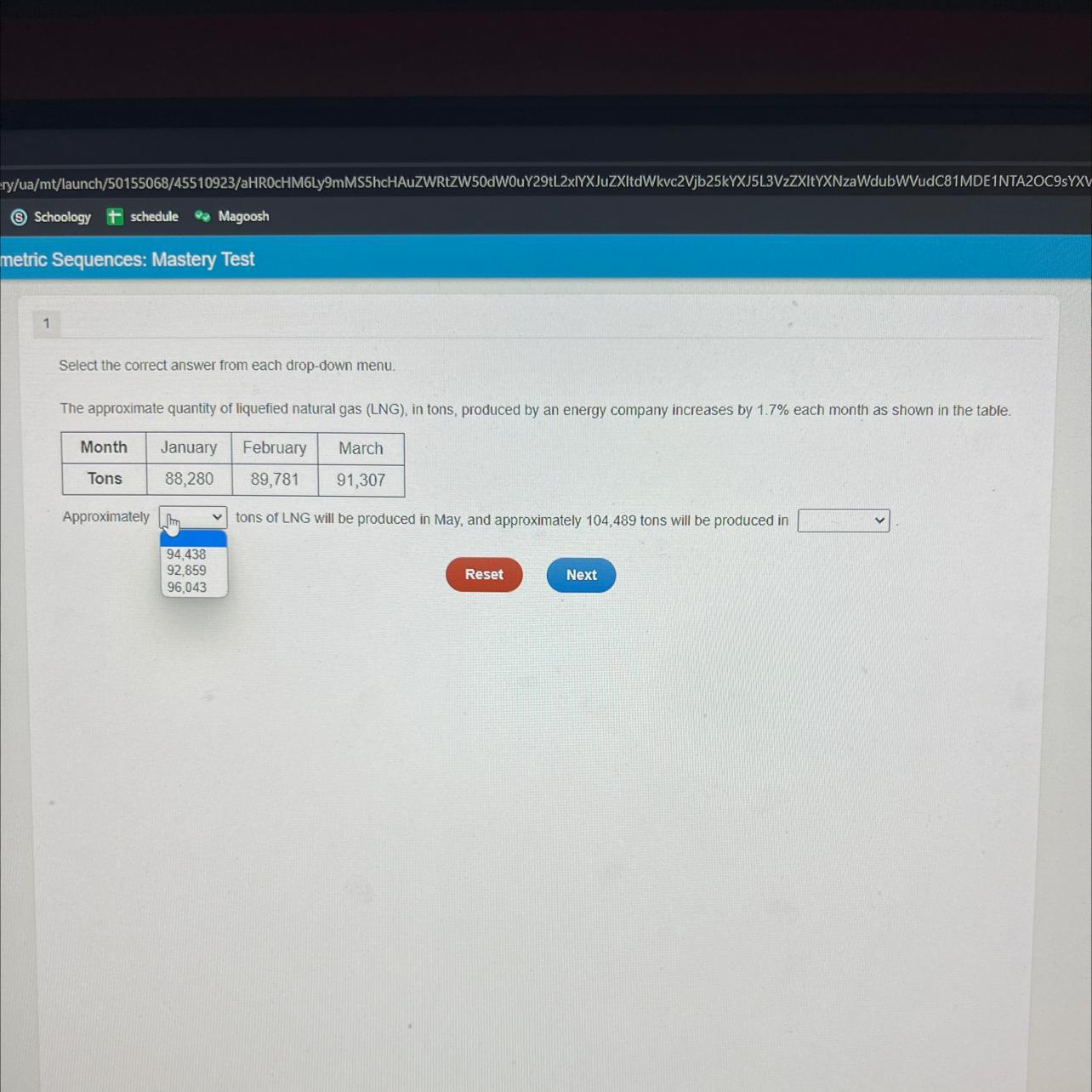
Select the correct answer from each drop-down menu.
The approximate quantity of liquefied natural gas (LNG), in tons, produced by an energy company increases by 1.7% each month as shown in the table.
January
88,280
Month
Tons
Approximately
February
March
89,781
91,307
tons of LNG will be produced in May, and approximately 104,489 tons will be produced in
Answers
Approximately 94,358 tons of LNG will be produced in May based on the given 1.7% monthly increase.
The given problem states that the approximate quantity of liquefied natural gas (LNG) produced by an energy company increases by 1.7% each month. We are given the production numbers for January, February, and March, and we need to calculate the approximate production for May.
To solve this problem, we can start with the production quantity in January, which is given as 88,280 tons. We then apply a 1.7% increase each month to find the production for subsequent months.
In February, the production can be calculated by multiplying the previous month's production by 1.017 (1 + 1.7%):
February production = 88,280 * 1.017 = 89,781 tons (rounded to the nearest whole ton).
Similarly, for March, we multiply the February production by 1.017:
March production = 89,781 * 1.017 = 91,307 tons (rounded to the nearest whole ton).
To find the production for May, we continue the pattern of applying a 1.7% increase:
April production = March production * 1.017 = 91,307 * 1.017 = 92,823 tons (rounded to the nearest whole ton).
Finally, we calculate the May production using the same method:
May production = April production * 1.017 = 92,823 * 1.017 = 94,358 tons (rounded to the nearest whole ton).
For more such information on: LNG
https://brainly.com/question/32004778
#SPJ8
Related Questions
Suppose that the efficacy of a certain drug 0.5. Consider the sampling distribution (sample size n-187) for the proportion of patients cured by this drug. What is the mean of this distribution?
What is the standard error of this distribution? (Round answer to four decimal places.)
Answers
The mean of the distribution is 0.5, and the standard error of the distribution is 0.0327.
Sampling distribution refers to the probability distribution that results from taking a large number of samples.
It provides information on the probability distribution of the sample's statistics.
If the efficacy of a drug is 0.5, and the sample size n-187, then the proportion of patients cured by the drug is expected to be 0.5.
The mean of the distribution of the proportion of patients cured by the drug is equal to the proportion of patients cured by the drug, which is 0.5.
The standard error of the distribution is the square root of the product of the variance of the proportion of patients cured by the drug, which is 0.25, and the reciprocal of the sample size.
So, the standard error is = √(0.25/187)
= 0.0327 (rounded to four decimal places).
Therefore, the mean of the distribution is 0.5, and the standard error of the distribution is 0.0327.
To know more about Sampling distribution visit:
brainly.com/question/31465269
#SPJ11
The vector q = (0,5,-3) starts at the point P=(-1,0,5). At what point does the vector end?
Answers
The vector q = (0, 5, -3) starts at the point P = (-1, 0, 5).We need to add the components of the vector to the coordinates of the starting point the vector q = (0, 5, -3) ends at the point (-1, 5, 2).
The vector q = (0, 5, -3) has three components: one for each coordinate axis (x, y, and z). We add these components to the corresponding coordinates of the starting point P = (-1, 0, 5) to find the coordinates of the endpoint.
Adding the x-component, 0, to the x-coordinate of P, -1, gives us -1 + 0 = -1. Therefore, the x-coordinate of the endpoint is -1.
Adding the y-component, 5, to the y-coordinate of P, 0, gives us 0 + 5 = 5. Thus, the y-coordinate of the endpoint is 5.
Adding the z-component, -3, to the z-coordinate of P, 5, yields 5 + (-3) = 2. Consequently, the z-coordinate of the endpoint is 2.
Therefore, the vector q = (0, 5, -3) ends at the point (-1, 5, 2).
To learn more about components of the vector click here : brainly.com/question/1686398
#SPJ11
The number of weeds in your garden grows exponential at a rate of 15% a day. if there were initially 4 weeds in the garden, approximately how many weeds will there be after two weeks? (Explanation needed)
Answers
After two weeks, there will be approximately 28 weeds in the garden.
How to determine how many weeds will there be after two weeksGiven that the weeds grow exponentially at a rate of 15% per day, we can express the growth factor as 1 + (15% / 100%) = 1 + 0.15 = 1.15. This means that the number of weeds will increase by 15% every day.
To calculate the number of weeds after two weeks, we need to apply the growth factor for 14 days starting from the initial value of 4 weeds:
Day 1: 4 x 1.15 = 4.6 (rounded to the nearest whole number)
Day 2: 4.6 x 1.15 = 5.29 (rounded to the nearest whole number)
Day 3: 5.29 x 1.15 = 6.08 (rounded to the nearest whole number)
...
Day 14: (calculate based on the previous day's value)
Continuing this pattern, we can calculate the number of weeds after each day, multiplying the previous day's value by 1.15.
Day 14: 4 x (1.15)^14 ≈ 27.8 (rounded to the nearest whole number)
Therefore, after two weeks, there will be approximately 28 weeds in the garden.
Learn more about exponential at https://brainly.com/question/2456547
#SPJ1
What is the limit of the sequence ⍺n = (n²-1/n²+1)n ?
a. 0
b. 1
c. e
d. 2
e. limit does not exist
Answers
The limit of the sequence ⍺n = ((n²-1)/(n²+1))n as n approaches infinity is (a) 0.
To find the limit of the sequence, we can simplify the expression ⍺n = ((n²-1)/(n²+1))n:
⍺n = ((n²-1)/(n²+1))n = (n²-1)n / (n²+1)
As n approaches infinity, we can ignore the lower-order terms in the numerator and denominator. Thus, we have:
⍺n ≈ n³/n² = n
Since the limit of n as n approaches infinity is infinity, the limit of the sequence ⍺n is also infinity. Therefore, the correct statement is (e) the limit does not exist.
However, if the sequence were modified to be ⍺n = ((n²-1)/(n²+1))n², the limit would be different. In that case, simplifying the expression would give:
⍺n = ((n²-1)/(n²+1))n² = (n²-1)n² / (n²+1)
Again, as n approaches infinity, we can ignore the lower-order terms, resulting in:
⍺n ≈ n⁴/n² = n²
In this case, the limit of the sequence ⍺n would be infinity as n approaches infinity.
Learn more about sequence here:
https://brainly.com/question/30262438
#SPJ11
Which set up would solve the system for y using Cramer's rule? 4x - 6y = 4 x + 5y = 14 A. y = |4 -6|
|1 5| / 26
B. y = |4 4|
|1 14| / 26
C. y = |4 -6|
|14 5| / 26
D. y = |4 -6|
|4 14| / 26
Answers
The set-up that would solve the system for y using Cramer's rule is:y = |4 -6||14 5| / 26
First, we find the determinant of the coefficient matrix:|4 -6|
|1 5|= (4 × 5) - (1 × -6) = 26Then, we replace the second column of the coefficient matrix with the constants from the equation:y = |4 -6|
|1 14| / 26Now, we find the determinant of the modified matrix:|4 4|
|1 14|= (4 × 14) - (1 × 4) = 52
Finally, we divide this determinant by the determinant of the coefficient matrix to get the value of y:y = 52/26 = 2Therefore, the correct set-up is:y = |4 -6||14 5| / 26.
#SPJ11
https://brainly.com/question/31694140
Evaluate the following integral using cylindrical coordinates: •∫-4 4 ∫ 0 √/16–x² ∫0 x x dz dy dx
Answers
To evaluate the given triple integral using cylindrical coordinates, we will first express the integral limits and differential elements in terms of cylindrical coordinates.
The integral is given as follows:
∫∫∫ x dz dy dx over the region D: -4 ≤ x ≤ 4, 0 ≤ y ≤ √(16 - x²), 0 ≤ z ≤ x In cylindrical coordinates, the conversion formulas are:
x = ρcos(θ)
y = ρsin(θ)
z = z
where ρ represents the radial distance and θ represents the angle in the xy-plane. Applying these transformations, we can rewrite the given integral as:
∫∫∫ ρcos(θ) dz dρ dθ
Next, we need to determine the limits of integration in terms of cylindrical coordinates. The limits for ρ, θ, and z are as follows:
-4 ≤ x ≤ 4 corresponds to -4 ≤ ρcos(θ) ≤ 4, which gives -4/ρ ≤ cos(θ) ≤ 4/ρ
0 ≤ y ≤ √(16 - x²) corresponds to 0 ≤ ρsin(θ) ≤ √(16 - ρ²cos²(θ))
0 ≤ z ≤ x remains the same.
Now we can rewrite the triple integral in cylindrical coordinates and evaluate it:
∫∫∫ ρcos(θ) dz dρ dθ
= ∫[0 to 2π] ∫[0 to √(16 - ρ²cos²(θ))] ∫[0 to ρ] ρcos(θ) dz dρ dθ
Evaluating this integral will involve integrating with respect to z first, then ρ, and finally θ, while respecting the given limits of integration. The final result will provide the numerical value of the triple integral.
Learn more about integrals here: brainly.com/question/4615818
#SPJ11
let f{o) = 0, /(1) = 1, /(2) = 22 , /(3) = 333 = 327, etc. in general, f(n) is written as a stack n high, of n's as exponents. show that f is primitive recursive.
Answers
So, g(n) is primitive recursive, as required.
In order to show that f is primitive recursive, we must first show that the function which outputs a stack n high of n's as exponents is primitive recursive.
Let's call this function g(n). Here's the definition:g(0) = 1g(n+1) = n ^ g(n)This can be translated into a recursive function using the successor and exponentiation functions:
g(0) = 1 g(n+1) = (n)^(g(n))
To show that g(n) is primitive recursive, we need to show that it can be constructed from the basic primitive recursive functions using composition, primitive recursion, and projection.
First, we'll need to define the basic primitive recursive functions.
Here's the list:
Successor: S(x) = x+1
Projection: pi_k^n(x1, ..., xn) = xk
Zero: Z(x) = 0
Here are the composition and primitive recursion rules:
Composition: If f: k_1 x ... x k_n -> m and g_1: m -> p_1 and ... and g_n:
m -> p_n are primitive recursive functions, then h:
k_1 x ... x k_n -> p_1 x ... x p_n defined by
h(x1, ..., xn) = (g_1(f(x1, ..., xn)), ..., g_n(f(x1, ..., xn)))
is a primitive recursive function.Primitive recursion:
If f: k_1 x ... x k_n x m -> m and
g: k_1 x ... x k_n -> m and
h: k_1 x ... x k_n x m x p -> p
are primitive recursive functions such that for all x1, ..., xn, we have f(x1, ..., xn, 0) = g(x1, ..., xn) and f(x1, ..., xn, m+1)
= h(x1, ..., xn, m, f(x1, ..., xn, m)), then k:
k_1 x ... x k_n x m -> m defined by k(x1, ..., xn, m) = f(x1, ..., xn, m) is a primitive recursive function.
Now we can show that g(n) is primitive recursive using these tools.
We'll use primitive recursion with base case Z(x) = 1 and recursive case f(n, g(n)). We define f as follows:
f(n, 0) = 1f(n, m+1)
=[tex]n ^ m[/tex] (using the exponentiation function)
Then we define g(n) = f(n, n).
It's clear that g(n) is the same function we defined earlier, and that f(n, m) is primitive recursive.
Therefore, g(n) is primitive recursive, as required.
to know more about primitive recursive visit:
https://brainly.com/question/32770070
#SPJ11
g(n) is the same function we defined earlier, and that f(n, m) is primitive recursive. Therefore, g(n) is primitive recursive, as required.
In order to show that f is primitive recursive, we must first show that the function which outputs a stack n high of n's as exponents is primitive recursive.
Let's call this function g(n). Here's the definition: [tex]g(0) = 1g(n+1) = n ^ g(n)[/tex].
This can be translated into a recursive function using the successor and exponentiation functions: [tex]g(0) = 1g(n+1) = n ^ g(n)\\[/tex].
To show that g(n) is primitive recursive, we need to show that it can be constructed from the basic primitive recursive functions using composition, primitive recursion, and projection.
First, we'll need to define the basic primitive recursive functions. Here's the list:
Successor: S(x) = x+1
Projection: [tex]pi_k^n(x1, ..., xn) = xk[/tex]
Zero: Z(x) = 0,
Here are the composition and primitive recursion rules:
Composition: If f: k_1 x ... x k_n -> m and g_1: m -> p_1 and ... and g_n: m -> p_n are primitive recursive functions,
then h: k_1 x ... x k_n -> p_1 x ... x p_n defined by
h(x1, ..., xn) = [tex](g_1(f(x1, ..., xn)), ..., g_n(f(x1, ..., xn)))[/tex]is a primitive recursive function.
Primitive recursion: If f: k_1 x ... x k_n x m -> m and
g: k_1 x ... x k_n -> m and
h: k_1 x ... x k_n x m x p -> p are primitive recursive functions such that for all x1, ..., xn,
we have [tex]f(x1, ..., xn, 0) = g(x1, ..., xn)[/tex]and [tex]f(x1, ..., xn, m+1) = h(x1, ..., xn, m, f(x1, ..., xn, m))[/tex], then
k: k_1 x ... x k_n x m -> m defined by
k(x1, ..., xn, m) = f(x1, ..., xn, m) is a primitive recursive function.
Now we can show that g(n) is primitive recursive using these tools. We'll use primitive recursion with base case Z(x) = 1 and recursive case f(n, g(n)). We define f as follows: [tex]f(n, 0) = 1f(n, m+1) = n ^ m[/tex] (using the exponentiation function).
Then we define g(n) = f(n, n).
To know more about exponents, visit:
https://brainly.com/question/5497425
#SPJ11
The principal Pla borrowed a simple Warest rate for a period of timet. Find the loan's future value A or the total amount ove at timet. Round answer to the nearest cent P-5000, 4.78%,te 5 months O A $6116 OB. 561680 OG 5612.95 OD 5742.50
Previous question
N
Answers
Given the principal (P) is 5000, simple interest (I) rate is 4.78%, and time (t) period is 5 months. the total amount of interest at time t is $ D.5,239.00.
We are required to calculate the loan's future value or the total amount of interest at the end of 5 months. This can be done using the formula for the future value of a simple interest, which is given as: FV = P + (P*I*t/100)Substitute the given values in the above formula to get:
FV = 5000 + (5000*4.78*5/100)FV
= 5000 + (1195/5)FV
= 5000 + 239FV
= $ 5,239.00
(approx)Therefore, the to the problem is that the loan's future value A or the total amount of interest at time t is $ 5,239.00. Hence, the option D is the correct answer.
To know more about principal visit:-
https://brainly.com/question/31725012
#SPJ11
Let A and B be events with P(4)=0.7, P (B)=0.4, and P(A or B)=0.8. (a) Compute P(A and B). (b) Are A and B mutually exclusive? Explain. (c) Are A and B independent? Explain.
Answers
(a) The value of P(A and B) is 0.3
(b) They are not mutually exclusive events
(c) They are not independent events
(a) How to determine the probability P(A and B)From the question, we have the following parameters that can be used in our computation:
P(4)=0.7, P (B)=0.4, and P(A or B)=0.8
The probability equation to calculate P(A and B) is represented as
P(A and B) = p(A) + p(B) - P(A or B)
Substitute the known values in the above equation, so, we have the following representation
P(A and B) = 0.7 + 0.4 - 0.8
Evaluate
P(A and B) = 0.3
Hence, the solution is 0.3
(b) Are A and B mutually exclusive?No, they are not mutually exclusive event
This is so because the event P(A and B) is not equal to 0
c) Are A and B independent?No, they are not independent event
This is so because the event P(A or B) is not equal to 0
Read more about probability at
brainly.com/question/24756209
#SPJ4
Decide whether the experiment is a binomial experiment. If it is not, explain why.
a.Test a cough suppressant using 600 people to determine if it is effective. You want to count the number of people who
find the cough suppressant to be effective.
b.You observe the gender of the next 850 babies born at a local hospital. The random variable represents the number of boys.
c.You draw a marble 350 times from a bag with three colors of marbles. The random variable represents the color of marble that is drawn.
Answers
a) Not binomial - Trials may not be independent.
b) Binomial - Fixed trials, independence, two outcomes.
c) Not binomial - Trials not independent, more than two outcomes for the random variable.
a) The experiment is not a binomial experiment because the conditions for a binomial experiment are not met. In a binomial experiment, there must be a fixed number of trials, each trial must be independent, there are only two possible outcomes (success or failure), the probability of success must remain constant for each trial, and the random variable of interest is the count of successes.
In this case, the number of people who find the cough suppressant effective is the random variable of interest, but the other conditions are not met. The trials may not be independent as the effectiveness of the cough suppressant could be influenced by factors such as individual health conditions or previous medication use.
b) The experiment is a binomial experiment because all the conditions for a binomial experiment are met. There is a fixed number of trials (850 births), each birth is independent of the others, there are two possible outcomes (boy or not a boy), the probability of having a boy is constant for each birth, and the random variable of interest is the count of boys.
c) The experiment is not a binomial experiment because the conditions for a binomial experiment are not met. In a binomial experiment, the trials must be independent, and each trial should have two possible outcomes.
In this case, the trials (drawing marbles) are not independent because the outcome of each draw affects the composition of the bag for subsequent draws. Additionally, the random variable of interest represents the color of the marble drawn, which has more than two possible outcomes (three colors).
To learn more about binomial experiment, click here: brainly.com/question/31646124
#SPJ11
Find the area of the regular polygon: Round your answer to the nearest tenth
Answers
The area of the shape is 105. 3 square units
How to determine the areaThe formula for calculating the area of a regular triangle is expressed as;
A =1/2 aP
This is so, such that the parameters of the formula are expressed as;
A is the area of the trianglea is the length of the apothemP is the perimeter of the triangleNote that perimeter is the sum of the lengths of the side.
Then, we have;
P= 15.6 + 15.6 + 15.6
add the values
P = 46.8 units
Substitute the value, we have;
Area = 1/2 × 4.5 × 46.8
Multiply the values, we get;
Area = 210.6/2
Divide the values
Area = 105. 3 square units
Learn more about area at: https://brainly.com/question/25292087
#SPJ1
(ii) Suppose that the following information was found in a partial fractions problem. Find the system of equations needed to solve for A, B, D, and E. Do not solve the system of equations. x³ 2x² + 3 = Ax³ - 3Ax - 5A + 2Bx² + 6Bx + Bx³ - 4Dx² + 10D 9Ex 15E x³ - 2x² + 3 = Ax³ + Bx³ + 2Bx² - 4Dx² - 3Ax + 6Bx - 9Ex - 5A+10D + 15E x³ 2x² + 3 = (A + B)x³ + (2B − 4D)x² + (−3A + 6B-9E)x - 5A + 10D + 15E SYSTEM OF EQUATIONS:
Answers
From the given information, we have the equation:
x³ + 2x² + 3 = (A + B)x³ + (2B - 4D)x² + (-3A + 6B - 9E)x - 5A + 10D + 15E
By equating the coefficients of like powers of x on both sides, we can form the following system of equations:
For x³ term:
1 = A + B
For x² term:
2 = 2B - 4D
For x term:
0 = -3A + 6B - 9E
For constant term:
3 = -5A + 10D + 15E
Therefore, the system of equations needed to solve for A, B, D, and E is:
A + B = 1
2B - 4D = 2
-3A + 6B - 9E = 0
-5A + 10D + 15E = 3
Solving this system of equations will give us the values of A, B, D, and E.
Learn more about partial fraction problems here:
https://brainly.com/question/30404141
#SPJ11
Let B= 1 1 -2 2 2 1 -2 2 1 2 -2 2 1 0 0 2 -1 0 0 0 -1 1 (a) With the aid of software, find the eigenvalues of B and their algebraic and geometric multiplicities.
Answers
The eigenvalues and their algebraic and geometric multiplicities of the given matrix B are[tex]:`λ = 2` -[/tex] algebraic multiplicity [tex]y = 1[/tex], geometric multiplicity [tex]= 1.`λ = -1` -[/tex] algebraic multiplicity [tex]y = 2[/tex], and geometric multiplicity = 0.
The given matrix is,`[tex]B=1 1 -2 2 2 1 -2 2 1 2 -2 2 1 0 0 2 -1 0 0 0 -1 1`[/tex]
We have to find the eigenvalues of the given matrix B.
To find the eigenvalues, we will find the determinant of[tex]`B-λI`[/tex] , where I is the identity matrix and λ is the eigenvalue.`
[tex]B-λI = (1-λ) 1 -2 2 2 1 -2 2 1 2 -2 2 1 0 0 2-λ -1 0 0 0 -1 1-λ`[/tex]
Expanding the determinant by the third row, we get:[tex]`(2-λ)[1 -2 2 1 -1 1-λ] - [0 -1 1-λ] + 0[0 -1 1-λ] = 0`[/tex]
Simplifying the above equation, we get:
[tex]`-λ³ + λ²(1+1+2) - λ(2(1-1-1)-2+0+0) + (2(1-1)+1(-1)(1-λ))=0`[/tex]
On solving the above cubic equation, we get eigenvalues as [tex]`λ = 2, -1, -1.`[/tex]
Now, we will find the algebraic and geometric multiplicities of the eigenvalues.
For this, we will subtract the given matrix by its corresponding eigenvalue multiplied by the identity matrix and then find its rank.`
i) For [tex]λ = 2:`B-2I = `[-1 1 -2 2 2 1 -2 2 1 2 -2 2 1 0 0 0 -1 0 0 0 -1 1][/tex]
`Rank of matrix `B-2I` is 2, which is equal to the algebraic multiplicity of the eigenvalue `λ = 2`.
Now, to find the geometric multiplicity of `[tex]λ = 2[/tex]`, we have to find the nullity of matrix `B-2I`.
nullity = number of columns - rank = 3 - 2 = 1.
Therefore, the geometric multiplicity of [tex]`λ = 2[/tex]` is 1.`ii) For [tex]λ = -1:`B-(-1)I = `[2 1 -2 2 2 1 -2 2 1 2 -2 2 1 0 0 2 0 0 0 0 0 1]`[/tex]
The rank of matrix `[tex]B-(-1)I` is 3[/tex], which is equal to the algebraic multiplicity of the eigenvalue `[tex]λ = -1`.[/tex]
Now, to find the geometric multiplicity of [tex]`λ = -1[/tex]`, we have to find the nullity of matrix `[tex]B-(-1)I[/tex]`.nullity = number of columns - rank [tex]= 3 - 3 = 0.[/tex]
Therefore, the geometric multiplicity of [tex]`λ = -1` is 0.[/tex]
Know more about eigenvalues here:
https://brainly.com/question/15586347
#SPJ11
I got P2(x) = 1/2x^2-x+x/2 but I have no idea how to find the error. Could you help me out and describe it in detail?
K1. (0.5 pt.) Let f (x) = |x − 1. Using the scheme of divided differences find the interpolating polynomial p2(x) in the Newton form based on the nodes to = −1, 1, x2 = 3.
x1 =
Find the largest value of the error of the interpolation in the interval [−1; 3].
Answers
The maximum value of the error is 0, and the polynomial P2(x) is an exact interpolating polynomial for f(x) over the interval [-1,3].
To find the error of the interpolation, you can use the formula for the remainder term in the Taylor series of a polynomial.
The formula is:
Rn(x) =[tex]f(n+1)(z) / (n+1)! * (x-x0)(x-x1)...(x-xn)[/tex]
where f(n+1)(z) is the (n+1)th derivative of the function f evaluated at some point z between x and x0, x1, ..., xn.
To apply this formula to your problem, first note that your polynomial is: P2(x) = [tex]1/2x^2 - x + x/2 = 1/2x^2 - x/2.[/tex]
To find the error, we need to find the (n+1)th derivative of f(x) = |x - 1|. Since f(x) has an absolute value, we will consider it piecewise:
For x < 1, we have f(x) = -(x-1).
For x > 1, we have f(x) = x-1.The first derivative is:
f'(x) = {-1 if x < 1, 1 if x > 1}.The second derivative is:
f''(x) = {0 if x < 1 or x > 1}.
Since all higher derivatives are 0, we have:
[tex]f^_(n+1)(x) = 0[/tex] for all n >= 1.
To find the largest value of the error of the interpolation in the interval [-1,3], we need to find the maximum value of the absolute value of the remainder term over that interval.
Since all the derivatives of f are 0, the remainder term is 0.
To know more about polynomial visit:
https://brainly.in/question/9172871
#SPJ11
find the indefinite integral. (use c for the constant of integration.) e2x 49 e4x dx
Answers
The value of the given integral is `1/2` e^(2x) + `49/4` e^(4x) + C.
The function is `e^(2x) + 49e^(4x)`.
To calculate the indefinite integral, follow the steps given below:
Step 1: Consider the integral ∫`e^(2x) + 49e^(4x) dx`
Step 2: Integrate the first term ∫`e^(2x) dx`We know that ∫e^u du = e^u + C. Here, u = 2x. Therefore, ∫`e^(2x) dx` = `1/2` ∫e^u du = `1/2` e^(2x) + C1, where C1 is the constant of integration.
Step 3: Integrate the second term ∫`49e^(4x) dx`We know that ∫e^u du = e^u + C. Here, u = 4x. Therefore, ∫`49e^(4x) dx` = `49/4` ∫e^u du = `49/4` e^(4x) + C2, where C2 is the constant of integration.
Step 4: Combine the results obtained in Step 2 and Step 3 to get the final result.∫`e^(2x) + 49e^(4x) dx` = `1/2` e^(2x) + `49/4` e^(4x) + C, where C is the constant of integration.
To know more about integration visit:
https://brainly.com/question/30094386
#SPJ11
The indefinite integral of the given function is:
∫(e^2x + 49e^4x) dx = (1/2)e^2x + (49/4)e^4x + c, where c is the constant of integration.
To find the indefinite integral of the given function, which is ∫(e^2x + 49e^4x) dx, we can apply the power rule for integration and the constant multiple rule. Here's the step-by-step solution:
∫(e^2x + 49e^4x) dx
Integrating e^2x:
∫e^2x dx = (1/2)e^2x + c₁ (Applying the power rule: ∫e^kx dx = (1/k)e^kx + C)
Integrating 49e^4x:
∫49e^4x dx = (49/4)e^4x + c₂ (Applying the power rule and constant multiple rule)
Combining the results:
∫(e^2x + 49e^4x) dx = (1/2)e^2x + c₁ + (49/4)e^4x + c₂
Since c₁ and c₂ are arbitrary constants, we can combine them into a single constant. Let's denote it as c:
∫(e^2x + 49e^4x) dx = (1/2)e^2x + (49/4)e^4x + c
Therefore, the indefinite integral of the given function is:
∫(e^2x + 49e^4x) dx = (1/2)e^2x + (49/4)e^4x + c, where c is the constant of integration.
To know more about indefinite integral, visit:
https://brainly.com/question/31617899
#SPJ11
if a parachutist lands at a random point on a line between markers a and b, find the probability that she is closer to a than to b. more than nine times her distance to b.
Answers
The correct answer is the probability that she is closer to a than to b is 0.5.Given that a parachutist lands at a random point on a line between markers a and b.
Also, it is given that her distance to b is more than nine times her distance to b.
Let the distance between a and b be denoted by AB. Let x be the distance of the parachutist from a.
Therefore, the distance of the parachutist from b is (AB - x)
Given that the distance of the parachutist from b is more than nine times her distance to b.
x < (AB - x)/9 => 10x < AB
i.e., 0 < x < AB/10
Therefore, the sample space for x is (0, AB/10).
The parachutist is closer to a than to b only if x < (AB - x).
i.e., x < AB/2
The probability that the parachutist lands between the points a and b such that she is closer to a than to b is the ratio of the length of the region OA to AB/10.
Therefore, required probability = OA / (AB/10)
= (AB/20) / (AB/10)
= 1/2
= 0.5.
Hence, the probability that she is closer to a than to b is 0.5.
To know more about probability, visit:
brainly.com/question/31828911
#SPJ11
2. Find the critical points, relative extrema, and saddle points. (a) f(x, y) = x³ + x - 4xy - 2y². (b) f(x, y) = x(y + 1) = x²y. (c) f(x, y) = cos x cosh y. [Note: The hyperbolic functions sinh and cosh are defined by sinh x = f[exp x exp(-x)], cosh x= [exp x + exp(-x)]. 2 (a) Maximum at e, + e₂, saddle point at (-e, + e₂). (b) Saddle points at - e₂ and at e₁ + €₂. (c) Saddle points at mле₁, m any integer.
Answers
The critical points, relative extrema, and saddle points of the given functions are given below:(a) f(x, y) = x³ + x - 4xy - 2y²Partial derivatives:fₓ(x, y) = 3x² + 1 - 4y, fₓₓ(x, y) = 6x,fₓᵧ(x, y) = -4,fᵧ(x, y) = -4y, fᵧᵧ(x, y) = -4
Critical point: Setting fₓ(x, y) and fᵧ(x, y) equal to zero, we get
3x² - 4y + 1 = 0 and -4x - 4y = 0S
This problem is related to finding the critical points, relative extrema, and saddle points of a function.
Here, we have three functions, and we need to find the critical points, relative extrema, and saddle points of each function.
Summary: The given functions are(a) f(x, y) = x³ + x - 4xy - 2y² has a relative minimum at (1, 1) and a saddle point at (-e, e).(b) f(x, y) = x(y + 1) - x²y has two saddle points at (0, 0) and (1/2, -1).(c) f(x, y) = cos x cosh y has saddle points at each critical point, which is mπ, nπi.
Learn more about functions click here:
https://brainly.com/question/11624077
#SPJ11
Describe the transformations which have been applied to f(x)^2
to obtain g(x)=2-2(1/2x+3)^2
Answers
Given that f(x)² is the starting function, the following transformations have been applied to get g(x) = 2 - 2(1/2x + 3)²:
• Horizontal Translation• Reflection about the x-axis• Vertical Translation• Vertical Stretch or Compression
Horizontal Translation: The graph of the function has been moved three units leftward to get a new graph.
There has been a horizontal translation of 3 units in the negative direction.
This has changed the location of the vertex.
The sign of the horizontal translation is always the opposite of what is written, in this case, -3.
Reflection about x-axis: The reflection of a function about the x-axis causes the function to be inverted upside down.
Therefore, the sign of the entire function changes.
Since this is a square term, it is not affected.
Therefore, it is just 2 multiplied by the square term.
Therefore, the function becomes -2(f(x))².
Vertical Translation: The graph of the function has been moved two units downward to get a new graph.
There has been a vertical translation of 2 units in the negative direction.
This has changed the location of the vertex.
Vertical Stretch or Compression: Since the coefficient -2 in front of the function term is negative, this reflects about the x-axis and compresses the parabola along the y-axis, with the vertex as the fixed point.
The graph of f(x)² is transformed into g(x) by changing the sign, horizontally shifting it by 3 units, vertically translating it down 2 units, and reflecting it about the x-axis.
To know more about Horizontal Translation, visit:
https://brainly.com/question/31938343
#SPJ11
Let f(x, y) = 4x² + 4xy + y².
Then a standard equation for the tangent plane to the graph of f at the point (-1, 1, 1) is
Answers
The standard equation for the tangent plane to the graph of `f(x, y) = 4x² + 4xy + y²` at the point `(-1, 1, 1)` is `z = -4x + 2y + 1`.
To find the standard equation of the tangent plane to the graph of a given function `f(x,y)` at a point `P(x₀,y₀,z₀)`, we use the following steps:
Find the partial derivatives of `f(x,y)` with respect to `x` and `y` as `fₓ(x,y)` and `fᵧ(x,y)`, respectively.
Evaluate `f(x,y)` at the given point `P(x₀,y₀,z₀)` to get `f(x₀,y₀) = z₀`.Plug the values of `x₀, y₀, z₀, fₓ(x₀,y₀)`, and `fᵧ(x₀,y₀)` into the following standard equation for the tangent plane:`z - z₀ = fₓ(x₀,y₀)(x - x₀) + fᵧ(x₀,y₀)(y - y₀)`
Now, let's use these steps to find the standard equation of the tangent plane to the graph of `f(x,y) = 4x² + 4xy + y²` at the point `(-1,1,1)`:
Partial derivatives of `f(x,y)` are:`fₓ(x,y) = ∂f/∂x = 8x + 4y``fᵧ(x,y) = ∂f/∂y = 4x + 2y`
Evaluate `f(x,y)` at the point `(-1,1,1)`:`f(-1,1) = 4(-1)² + 4(-1)(1) + 1² = -3`So, `x₀ = -1`, `y₀ = 1`, and `z₀ = -3`.
Substitute these values, and `fₓ(x₀,y₀) = 8(-1) + 4(1) = -4`, and `fᵧ(x₀,y₀) = 4(-1) + 2(1) = 2`into the standard equation of the tangent plane:
`z - (-3) = -4(x - (-1)) + 2(y - 1)`
Simplify and write in standard form:`z = -4x + 2y + 1`
Therefore, the standard equation for the tangent plane to the graph of `f(x, y) = 4x² + 4xy + y²` at the point `(-1, 1, 1)` is `z = -4x + 2y + 1`.
Learn more about tangent plane at:
https://brainly.com/question/30885019
#SPJ11
Mr. Cross, Mr. Jones, and Mr. Smith all suffer from coronary heart disease. As part of their treatment, they were put on special low-cholesterol diets: Cross on Diet I, Jones on Diet II, and Smith on Diet III. Progressive records of each patient's cholesterol level were kept. At the beginning of the first, second, third, and fourth months, the cholesterol levels of the three patients were as follows:
Cross: 220,215,210220,215,210, and 205205
Jones: 220,210,200220,210,200, and 195195
Smith: 215,205,195215,205,195, and 190190
a. Represent this information using a 3×43×4 matrix A. Find a24 and explain its meaning.
b. Represent this information using a 4×34×3 matrix B. Find b32 and explain its meaning.
Answers
a)Matrix A represents the cholesterol levels of Cross, Jones, and Smith over four months. The entry a24 in matrix A represents the cholesterol level of Cross in the second row and fourth column, which is 205. It indicates Cross's cholesterol level in the second month of the observation.
b) Matrix B represents the cholesterol levels of Cross, Jones, and Smith over three months. The entry b32 in matrix B represents the cholesterol level of Smith in the third row and second column, which is 205. It indicates Smith's cholesterol level in the second month of the observation.
What is the meaning of the entries a24 and b32 in the matrices A and B, respectively?In matrix A, the rows correspond to the three patients (Cross, Jones, and Smith), and the columns represent the months. Each entry in matrix A represents the cholesterol level of a specific patient in a specific month. For example, the entry a24 represents Cross's cholesterol level in the second month.
Similarly, in matrix B, the rows correspond to the months, and the columns represent the patients. Each entry in matrix B represents the cholesterol level of a specific month for a specific patient. For instance, the entry b32 represents Smith's cholesterol level in the second month.
By organizing the cholesterol level data in matrices A and B, it becomes easier to analyze and compare the changes in cholesterol levels over time for each patient. These matrices provide a concise and structured representation of the patients' cholesterol data, facilitating further analysis and interpretation.
Learn more about matrices
brainly.com/question/30646566
#SPJ11
1. Suppose a festival game of chance runs as follows:
A container full of tokens is presented to the player. The player must reach into the container and blindly select a token at random. The player holds on to this token (i.e. does not return it to the container), and then blindly selects a second token at random from the container.
If the first token drawn is green, and the second token drawn is red, the player wins the game. Otherwise, the player loses the game.
Suppose you decide to play the game, and that the container contains 44 tokens, consisting of 22 green tokens, 19 red tokens, and 3 purple tokens.
To help with this question, we define two key events using the following notation:
⚫ G1 denotes the event that the first token selected is a green token.
R2 denotes the event that the second token selected is a red token.
Using the information above, answer the following questions.
(a) Calculate P(G1).
(b) Calculate P(R2G1).
(c) Calculate P(G1 and R2). Make sure you show all your workings.
(2 marks)
(2 marks)
(3 marks)
(d) Is it more likely that you will win, or lose, this game? Explain the reasoning behind your answer, with reference to the previous result.
(1 mark)
(e) If the three purple tokens were removed from the game, what is the probability of winning the game? Make sure you show all your workings.
(4 marks) (f) Suppose that the designer of the game would like your probability of winning to be at least 0.224, (i.e. for you to have at least a 22.4% chance of winning). If the number for green and purple tokens remains the same as the initial scenario (22 and 3 respectively), but a new, different number of red tokens was used, what is the smallest total number of tokens (all colours) needed to achieve the desired probability of success of 0.224 or higher?
Make sure to very clearly explain your thought processes, and how you obtained your answer.
Answers
(a) The probability of selecting a green token first is 22/44, which is equal to 0.5.
(b) P(R2G1) is the probability of selecting a red token second, given that a green token was selected first. So, after selecting the green token, there will be 43 tokens left, including 21 green tokens and 19 red tokens.
Therefore, the probability of selecting a red token second, given that a green token was selected first, is 19/43, which is approximately equal to 0.442.
(c) P(G1 and R2) is the probability of selecting a green token first and a red token second. Using the multiplication rule, we can calculate this as follows: P(G1 and R2) = P(G1) × P(R2G1)
P(G1 and R2) = 0.5 × 0.442
P(G1 and R2) = 0.221 or approximately 0.22
(d) The probability of winning the game is 0.22, which is less than 0.5. Therefore, it is more likely to lose the game. This is because the probability of selecting a red token first is 19/44, which is greater than the probability of selecting a green token first (22/44). Therefore, even if a player selects a green token first, there is still a high probability that they will select a red token second and lose the game.
(e) If the three purple tokens are removed from the game, there will be 41 tokens left, including 22 green tokens and 19 red tokens. Therefore, the probability of winning the game is:
P(G1 and R2) = P(G1) × P(R2G1)
P(G1 and R2) = 22/41 × 19/40
P(G1 and R2) = 209/820
P(G1 and R2) is approximately 0.255.
(f) Let x be the number of red tokens needed to achieve a probability of winning of 0.224 or higher. Then, we can set up the following equation using the values we know:
0.224 ≤ P(G1 and R2) = P(G1) × P(R2G1)
0.224 ≤ 22/(x + 22) × (x/(x + 21))
Simplifying this inequality, we get:
0.224 ≤ 22x/(x + 22)(x + 21)
0.224(x + 22)(x + 21) ≤ 22x
0.224x² + 10.528x + 4.704 ≤ 22x
0.224x² - 11.472x + 4.704 ≤ 0
We can solve this quadratic inequality by using the quadratic formula:
x = [11.472 ± √(11.472² - 4 × 0.224 × 4.704)]/(2 × 0.224)
x = [11.472 ± 8.544]/0.448
x ≈ 46.18 or x ≈ 2.32
The smallest total number of tokens needed to achieve a probability of winning of 0.224 or higher is 46 (since the number of tokens must be a whole number). Therefore, if there are 22 green tokens, 3 purple tokens, and 21 red tokens, there will be a probability of winning of approximately 0.228.
To know more about Quadratic inequality visit-
brainly.com/question/6069010
#SPJ11
The 10, 15, 20, or 25 Year of Service employees will receive a milestone bonus. In Milestone Bonus column uses the Logical function to calculate Milestone Bonus (Milestone Bonus = Annual Salary * Milestone Bonus Percentage) for the eligible employees. For the ineligible employees, the milestone bonus will equal $0. Please find the Milestone Bonus Percentage in the " Q23-28" Worksheet. Change the column category to Currency and set decimal to 2.
Answers
To calculate the Milestone Bonus, use the formula Milestone Bonus = Annual Salary * Milestone Bonus Percentage. Set the column category to Currency and decimal to 2. Ineligible employees will receive a milestone bonus of $0.
The Milestone Bonus for eligible employees is calculated by multiplying their Annual Salary by the Milestone Bonus Percentage. To find the appropriate Milestone Bonus Percentage, you need to refer to the "Q23-28" Worksheet, which contains the necessary information. Once you have obtained the percentage, apply it to the Annual Salary for each eligible employee.
To ensure clarity and consistency, it is recommended to change the column category for the Milestone Bonus to Currency. This formatting choice allows for easy interpretation of monetary values. Additionally, set the decimal precision to 2 to display the Milestone Bonus with two decimal places, providing accurate and concise information.
It is important to note that ineligible employees, for whom the Milestone Bonus does not apply, will receive a milestone bonus of $0. This ensures that only employees meeting the specified service requirements receive the additional compensation.
Learn more about Milestone
brainly.com/question/29956477
#SPJ11
2. Set up a triple integral to find the volume of the solid that is bounded by the cone Z= z =√√x² + y² and the sphere.x² + y² +z² = 8.
Answers
To set up a triple integral to find the volume of the solid bounded by the given cone and sphere, we need to express the limits of integration for each variable.
Let's consider the given equations: z = √√x² + y² (equation of the cone) and x² + y² + z² = 8 (equation of the sphere). We can rewrite the equation of the cone as z = (x² + y²)^(1/4). Notice that the cone is symmetric with respect to the z-axis, so we can focus on the region where z ≥ 0.
Now, let's determine the limits of integration for each variable. Since the cone is symmetric, we can consider only the region where x ≥ 0 and y ≥ 0. For the sphere, we can use spherical coordinates to simplify the calculation.In spherical coordinates, the equation of the sphere becomes r² = 8. We can set up the following limits: 0 ≤ r ≤ 2√2 (from the equation of the sphere), 0 ≤ θ ≤ π/2 (to cover the region where x ≥ 0), and 0 ≤ φ ≤ π/4 (to cover the region where y ≥ 0).Now, we can set up the triple integral to find the volume:V = ∫∫∫ f(x, y, z) dV= ∫∫∫ 1 dV= ∫₀^(π/4) ∫₀^(π/2) ∫₀^(2√2) r² sin φ dr dθ dφ
Integrating with respect to r, θ, and φ over their respective limits will give us the volume of the solid bounded by the cone and sphere.In summary, the triple integral to find the volume of the solid is V = ∫₀^(π/4) ∫₀^(π/2) ∫₀^(2√2) r² sin φ dr dθ dφ. By evaluating this integral, we can determine the volume of the solid.
To learn more about limits of integration click here:
brainly.com/question/31994684
#SPJ11
8. a. Find an equation of the tangent plane to the surface y²z³-10=-x³z at the point P(1,-1, 2). b. Find an equation of the tangent plane to the surface xyz' =-z-5 at the point P(2, 2, -1).
Answers
a. The equation of the tangent plane to the surface y²z³ - 10 = -x³z at the point P(1, -1, 2) is 2x + 3y + 9z = 37.
b. The equation of the tangent plane to the surface xyz' = -z - 5 at the point P(2, 2, -1) is 4x + 2y - z = -17.
a. To find the equation of the tangent plane to the surface y²z³ - 10 = -x³z at the point P(1, -1, 2), we need to calculate the partial derivatives of the surface equation with respect to x, y, and z, evaluate them at the given point, and then use these values to construct the equation of the plane.
The partial derivatives are:
∂F/∂x = -3x²z,
∂F/∂y = 2yz³,
∂F/∂z = 3y²z² - 10.
Evaluating these derivatives at P(1, -1, 2), we get:
∂F/∂x(1, -1, 2) = -3(1)²(2) = -6,
∂F/∂y(1, -1, 2) = 2(-1)(2)³ = -32,
∂F/∂z(1, -1, 2) = 3(-1)²(2)² - 10 = 2.
Using the point-normal form of a plane equation, the equation of the tangent plane becomes:
-6(x - 1) - 32(y + 1) + 2(z - 2) = 0,
which simplifies to 2x + 3y + 9z = 37.
b. To find the equation of the tangent plane to the surface xyz' = -z - 5 at the point P(2, 2, -1), we follow a similar process. The partial derivatives are:
∂F/∂x = yz',
∂F/∂y = xz',
∂F/∂z = xy' - 1.
Evaluating these derivatives at P(2, 2, -1), we get:
∂F/∂x(2, 2, -1) = 2(-1) = -2,
∂F/∂y(2, 2, -1) = 2(-1) = -2,
∂F/∂z(2, 2, -1) = 2(2)(0) - 1 = -1.
Using the point-normal form, the equation of the tangent plane becomes:
-2(x - 2) - 2(y - 2) - 1(z + 1) = 0,
which simplifies to 4x + 2y - z = -17.
To learn more about tangent plane visit:
brainly.com/question/31433124
#SPJ11
1. The random variables X, Y have joint probability mass function
fx.y(x, y) = 361 if x,y (1,2,3), otherwise.
(a) Find the marginal p.m.f.'s fx(x) and fy(y).
(b) Let A be the event that X + Y is divisible by 4. Compute P(A).
(c) Compute E(XY).
(d) Are X and Y independent? Justify your answer.
(e) Find the conditional probability mass function fxy=1)(x) = P(X = Y = 1) for all x.
(f) Compute the conditional expected value of X given Y = 1, that is, E(XY = 1) for all value of x.
(g) Compute the covariance of X and Y, Cov(X, Y).
(h) Compute the correlation of X and Y, i.e., Px.Y.
(i) From your answer to (g), what can you say about the relationship of X and Y in one to two sentences.
(j) Let Z=X+aY where a is a constant. Determine the value of a that makes Z and Y uncorrelated.
Answers
(a) The marginal p.m.f.'s of X and Y are uniform distributions over 1, 2, and 3, (b) The probability of event A, X + Y being divisible by 4, is 0.694, (c) E(XY) = 7.194, (d) X and Y are independent, (e) The conditional p.m.f. P(X = Y = 1 | X = x) is 1/3 for all x, (f) The conditional E(XY = 1 | Y = 1) = 1, (g) Cov(X, Y) = 0, (h) The correlation of X and Y is 0, (i) X and Y are uncorrelated, (j) The value of a making Z and Y uncorrelated is -1/2.
(a) Marginal p.m.f.'s are found by summing the joint p.m.f. over the relevant values. In this case, the joint p.m.f. is constant, resulting in uniform distributions for X and Y.
(b) P(A) is computed by identifying (x, y) pairs where X + Y is divisible by 4. The probability of these pairs yields P(A) = 0.694.
(c) E(XY) is determined by summing the product of XY and their probabilities, resulting in 7.194.
(d) X and Y are independent because the joint p.m.f. can be factored into the product of the marginal p.m.f.'s.
(e) The conditional p.m.f. P(X = Y = 1 | X = x) is consistently 1/3 for all x.
(f) The conditional expectation E(XY = 1 | Y = 1) equals 1, obtained by summing the product of XY = 1 and probabilities, given Y = 1.
(g) Cov(X, Y) = 0, indicating no linear relationship.
(h) The correlation between X and Y is 0, implying no linear association.
(i) X and Y are uncorrelated, indicating no linear dependence.
(j) The value of a for Z = X + aY to be uncorrelated with Y is -1/2.
To learn more about independent click here: brainly.com/question/15375461
#SPJ11
Use the double angle identity sin (20) 2 sin (0) cos(0) to express the following using a single sine function. 8 sin (7x) cos(7x) Submit Question
Answers
The double angle identity sin(2θ) = 2sin(θ)cos(θ) can be utilized to show that 8sin(7x)cos(7x) is equal to 4[2sin(7x)cos(7x)] = 4sin(14x).
Step by step answer:
The given identity is sin(2θ) = 2sin(θ)cos(θ)
The given equation is 8sin(7x)cos(7x)
As per the identity sin(2θ) = 2sin(θ)cos(θ) ,
this equation can be re-written as: 8sin(7x)cos(7x) = 2 x 4sin(7x)cos(7x)
Using the identity sin(2θ) = 2sin(θ)cos(θ),
we can simplify 4sin(7x)cos(7x) as:4sin(7x)cos(7x)
= sin(2x7x)
Therefore, 8sin(7x)cos(7x) = 2 x sin(2x7x)
= 4sin(14x).
Thus, we can use the double angle identity sin(20) 2 sin(0) cos(0) to express 8sin(7x)cos(7x) using a single sine function as 4sin(14x).
To know more about double angle identity visit :
https://brainly.com/question/30402758
#SPJ11
In three-space, find the distance between the skew lines: [x, y, z)= [1.-1. 1] + [3, 0, 4] and [x, y, z]= [1, 0, 1] + [3, 0, -1]. Express your answer to two decimals.
Answers
The distance between the skew lines is determined as 5.10.
What is the distance between the skew lines?The distance between the skew lines is calculated by applying the formula for distance between two points.
The resultant vector of the first two points is calculated as;
R = [x, y, z] = [1.-1. 1] + [3, 0, 4]
R = [(1 + 3), (-1 + 0), (1 + 4) ]
R = [4, -1, 5]
The resultant vector of the second two points is calculated as;
S = [x, y, z] = [1, 0, 1] + [3, 0, -1]
S = [ (1 + 3), (0 + 0), (1 - 1)]
S = [4, 0, 0]
The distance between point R and S is calculated as follows;
D = √[ (4 - 4)² + (-1 - 0)² + (5 - 0)² ]
D = √ (0 + 1 + 25)
D = √ 26
D = 5.10 units (two decimal places)
Learn more about distance between points here: https://brainly.com/question/7243416
#SPJ4
Written as a simplified polynomial in standard form, what is the result when (x+5)2 is subtracted from 1 ?
Answers
The simplified polynomial in standard form is - x² - 5x - 24
How to write the simplified polynomial in standard formFrom the question, we have the following parameters that can be used in our computation:
(x + 5)² is subtracted from 1
When represented as an expression, we have
1 - (x + 5)²
Open the brackets
1 - (x² + 5x + 25)
So, we have
1 - x² - 5x - 25
Using the above as a guide, we have the following:
- x² - 5x - 24
Hence, the simplified polynomial in standard form is - x² - 5x - 24
Read more about polynomial at
https://brainly.com/question/30833611
#SPJ1
Problem 1. The following table shows the result of a survey that asked a group of core gamers which gamming platform they preferred. Smartphone Console PC Total Male 51 35 43 129 Female 46 22 31 99 Total 97 57 74 228 If a gamer from this survey is chosen at random, find the probability that the gamer chosen: (a) [5 pts] is female. (b) 15 pts] prefers a console. 4
Answers
(a) To find the probability that the gamer chosen is female, we need to divide the number of female gamers by the total number of gamers.
From the table, we can see that the total number of female gamers is 99, and the total number of gamers (male + female) is 228.
Probability of choosing a female gamer = Number of female gamers / Total number of gamers
= 99 / 228
Therefore, the probability that the gamer chosen is female is 99/228.
(b) To find the probability that the gamer chosen prefers a console, we need to divide the number of gamers who prefer a console by the total number of gamers.
From the table, we can see that the number of gamers who prefer a console is 57, and the total number of gamers is 228.
Probability of choosing a gamer who prefers a console = Number of gamers who prefer a console / Total number of gamers
= 57 / 228
Therefore, the probability that the gamer chosen prefers a console is 57/228.
To learn more about probability visit: brainly.com/question/30034780
#SPJ11
Suppose you want to test the null hypothesis that β_2 is equal to 0.5 against the two-sided alternative that β_2 is not equal to 0.5. You estimated β_2= 0.5091 and SE (β_2) = 0.01. Find the t test statistic at 5% significance level and interpret your results (6mks).
Answers
The t test statistic is 0.91 and we fail to reject the null hypothesis.
How to calculate the t test statistic at 5% significance levelFrom the question, we have the following parameters that can be used in our computation:
β₂ = 0.5 against β₂ ≠ 0.5.
Estimated β₂ = 0.5091
SE (β₂) = 0.01.
The t test statistic at 5% significance level is calculated as
t = (Eβ₂ - β₂) / SE(β₂)
Substitute the known values in the above equation, so, we have the following representation
t = (0.5091 - 0.50) /0.01
Evaluate
t = 0.91
The results means that we fail to reject the null hypothesis.
Read more about test of hypothesis at
https://brainly.com/question/14701209
#SPJ4